Back • Return Home
Mother's Four-Fold Foundations
• Basic Square
• Other Members of The Quadrilateral Family
• Basic Octagon
• Octagrams & Their Decorative Variations
• The Sacred Cut, A Pattern Generator
• The Brunés Star, A Pattern Organizer
• A Historical Interlude: Math Like An Egyptian
• Squaring The Circle
Basic Square (4-Sided Shape)
A square is a type of "quadrilateral". The prefix "quad-" means "four" and the term "lateral" means "side", so a "quadrilateral" is a shape with four sides. However, please keep in mind that this term applies to more than just squares.
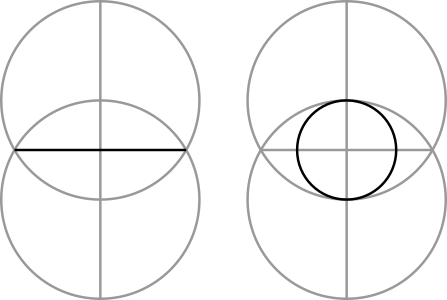
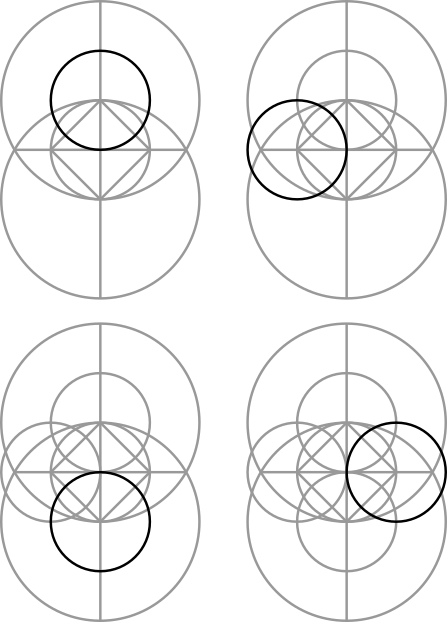
Step 1: This has the same beginning as the triangle construction that we covered before. Draw a vertical line and place a circle on it.
Step 2: Draw another circle of the same size centered on one of the points where the circle and the vertical line of the previous step cross.
Step 3: Use the two points where the circles overlap to draw a line, and use where those two lines overlap to draw a small circle.
Step 4: We now have enough points to draw a small square.
However, let's do this step a different way...
Alternate Step 4: Use the points where the small circle crosses the two lines to make two more lines that touch the circumference of the larger circle.
Alternate Step 5: We now have enough points to draw a larger square.
Other Members of The Quadrilateral Family
[Note: These instructions are adapated from the ones given on the HPTGN website by Robin Hu.]
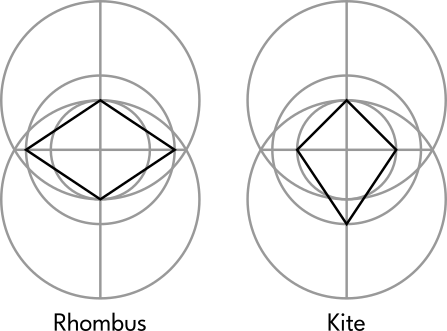
If we add another circle to Step 3 of the above construction, we can make a few other quadrilaterals. It doesn't matter what size the circle is, so long as it shares the same center as the small circle:
We can use all of these points to form both a rhombus and a kite:
Notice that all four corners of both shapes are touching one of the two circles. We can change the dimensions of the shapes by changing the size of the two circles relative to one another.
Three other quadrilaterals can be made by applying a similar process to any of the hexagon constructions. For example:
Basic Octagon (8-Sided Shape)
The prefix "oct-" means "eight". This can be thought of as an extension of the Basic Square construction given above.
After making the "X" in Step 5, use the the other points on the small circle to draw two more lines that touch the circumference of the larger circle:
This produces eight points on the circumference of the larger circle that we can use to make an octagon:
Octagrams & Their Decorative Variations
There is one unicursal octagram {8/3}:
There is also one compound octagram {8/2}. It is composed of two squares:
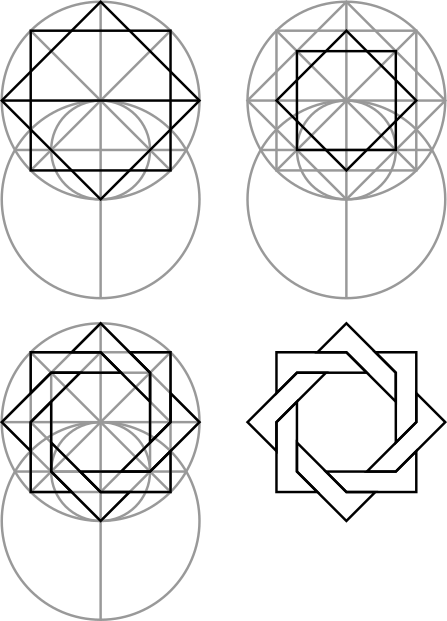
By adding more lines to the octagon construction, we can make a template for producing decorative variations of the octagram in a manner similar to what we did with the hexagrams:
The Sacred Cut, A Pattern Generator
To quote the fascinating article "A Secret of Ancient Geometry" by Jay Kappraff:
...Tons Brunés, a Danish engineer, [...] hypothesized a system of ancient geometry that he believed lay at the basis of many of the temples of antiquity. It was Brunés's belief that there existed until about 1400, a network of temples and a brotherhood of priests originating in ancient Egypt which had a secret system of geometry.
The system of geometry that Tons Brunés describes is simple, but powerful. We can generate a huge number of beautiful geometric patterns through it. And like The Flower of Life, an untold number of craftspersons the world over have used it to do so.
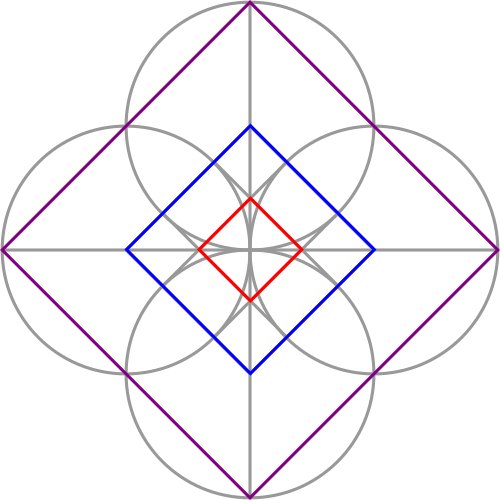
Picking up on Step 4 of our Basic Square construction, let's add four more circles that are the same size as our central circle:
These four circles divide up the central square into the following pattern:
Again, each arc can be thought of as simply a circle whose radius is half the diagonal of the square:
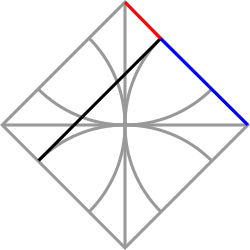
Connecting the arcs that are opposite one another with lines divides the sides of the square into "The Sacred Cut", a particular proportion that shows up in a lot of ancient art and architecture (shown here by the red and blue lines):
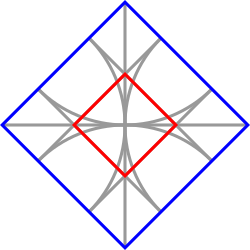
If we continue to draw lines from each arc to the one opposite, then we form a smaller square that is related to the larger square by that same proportion:
Extend the diagonals of the square until they meet the circumference of the circles that made the arcs. Then, connect them together with lines to make another square (shown here in purple):
All three of these squares are related to one another in The Sacred Cut proportion.
While all of this might seem complicated, we just want to give an idea of how to "contract" the pattern inwardly or "expand" it outwardly. In actuality, we don't have to understand any of the mathematics behind The Sacred Cut in order to use it effectively. Let's describe how...
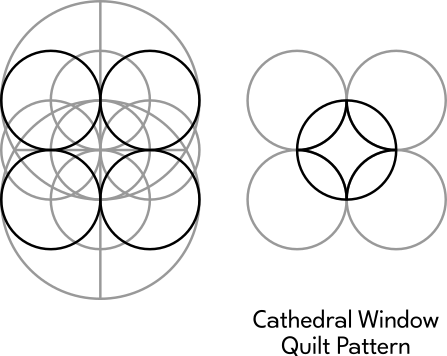
If we add four more circles to the figure that we used to generate The Sacred Cut square, it can be made into a well-known quilting pattern, aptly named a "cathedral window". It might seem familiar:
In her article "Behind the Pattern", a famous quiltmaker named Margit Echols describes how she used The Sacred Cut square as a template to design quilts. It contains a diagram similar to the following:
As she points out in another article, "An Elegant Solution" (also contained within the same document linked above):
Even though the shapes in this collection are familiar to quiltmakers, they are more commonly found in Islamic art than in quilts.
Why would these patterns show up in such radically different times and places?
While it may not seem like it sometimes, Nature is orderly. To paraphrase a belief of the spritual group, Builders of the Adytum:
Ageless Wisdom is not susceptible to the mutations of time, nor is it primarily a product of man's thinking. It is written by God upon the face of Nature, and is always there for men and women of all epochs to read, if they can.
Our motivation is beyond the aesthetic. Nature is an "open book" and an understanding of the geometric patterns that we are attempting to describe here can help us to "read it". This language transcends every culture, every race, every nation. All people whom have ever walked this Earth have a place within its design.
Many groups have found it necessary to put the knowledge that they acquired through lifetimes of Nature study into symbol and call it "sacred". Not only does this facilitate its transmission from generation-to-generation by making it easier to remember, it helps keep it from becoming lost or distorted. One method of doing this is to take something sacred and embed it within something "mundane", a familiar everyday item, like a quilt. The term "legominism" is sometimes used to describe such an item.
The item does not need to have a practical purpose in order for it to be considered a legominism. For example, upon its face, it might not be obvious that a game like chess could be a metaphor for the laws of Nature. A clear idea of its meaning has become blurred by the mists of time, yet people's enjoyment of it has ensured that some aspect of it has endured.
Unfortunately, there is also another reason why one would hide a treasure amongst something innocuous. Sometimes things are hidden, not because those who are hiding them do not want to share them, but because they are being actively persecuted for their beliefs. Preservation is the only hope that they have of ever being understood. So much of our own history as human beings is a time capsule waiting to be opened.
Onward, upward...
The Brunés Star, A Pattern Organizer
[This pattern appears in multiple works, such as Sacred Geometry by Miranda Lundy, Islamic Art and Architecture by Issam El-Said, Celtic Design: Knotwork by Aidan Meehan, etc.]
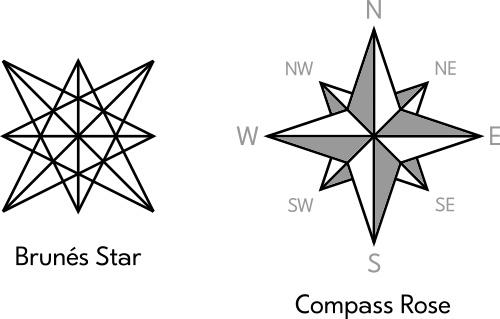
There is another aspect to the system of geometry pointed out by Tons Brunés. First, let's use the Basic Octagon construction to draw a square and a line instead of an octagon:
This gives us a square divided into four smaller squares (a 2 × 2 grid), like this:
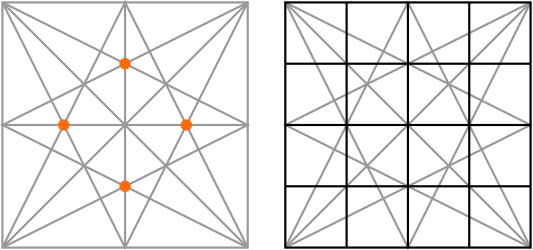
Next, let's draw "V"-like shapes from every pair of corners to the midpoints opposite:
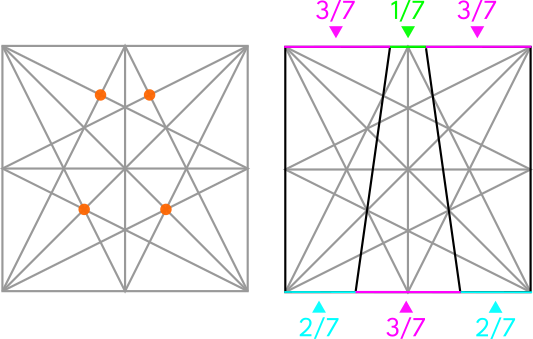
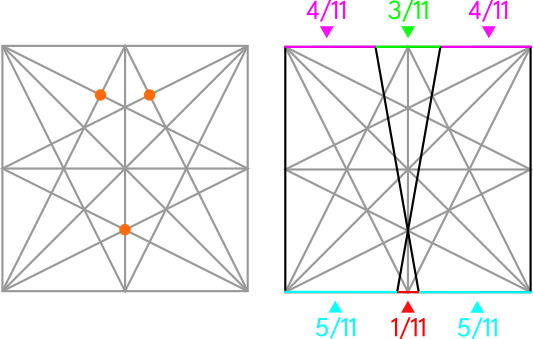
We end up with an octagram with four points that are smaller than the other four. This is called "The Brunés Star" and it looks like a "compass rose":
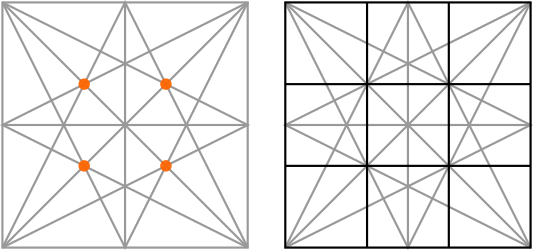
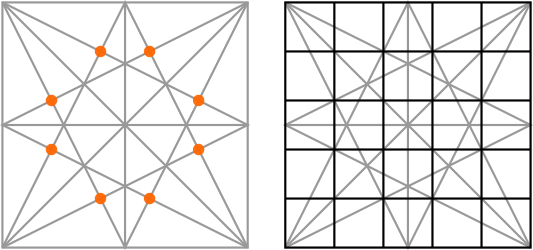
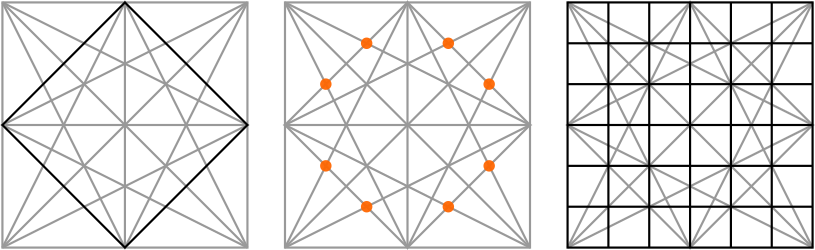
We can use where the lines of the star intersect to divide the sides of the square into particular increments or to create square grids of different sizes. For example:
• 3 × 3
• 4 × 4
• 5 × 5
Adding another square will give us points that we can use to make a 6 × 6 grid:
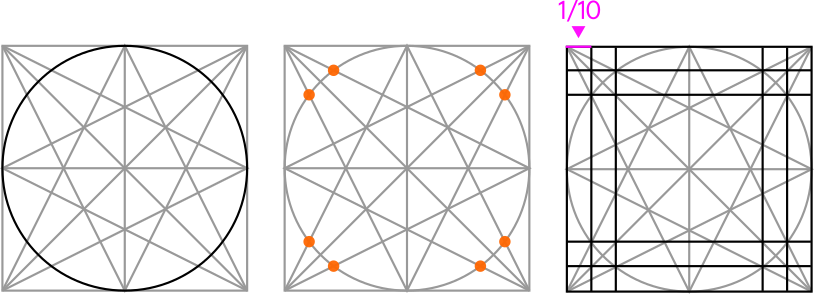
Adding a circle will give us points that we can use to divide the side of the square into tenths:
We can also divide the side of the square into some irregular divisions, such as sevenths:
...and elevenths:
All sorts of different divisions and grid sizes can be found by playing around with the above constructions or combining them (e.g.: we can divide the squares of the 4 × 4 grid in half to make an 8 × 8 grid). This diagram is sometimes called a "Starcut" for this reason.
It is a very useful tool. We will repeatedly apply it as we continue. Try generating grids with The Brunés Star, and then use The Sacred Cut method in the previous section to turn those squares into a decorative pattern.
A Historical Interlude: Math Like An Egyptian
[Please feel free to skip over this section if the topic does not interest you.]
Photo Credit: Jorge Láscar
[To the left is "The Sphinx" and the right is "The Pyramid of Chephren" on the Giza Plateau outside of Cairo, Egypt.]
The floor plans of the oldest temples on Earth were drawn directly on the ground upon which they were built. One's compass was simply two sticks. One stick is the "point" of a compass, planted firmly in the dirt to mark the center of our circle. The other stick is attached to it by a length of rope. This stick acts like the "pencil" of the compass, tracing out the circumference of the circle when the rope is pulled taught. We can control the radius of the circle by changing how much rope we use. In other words, using more rope makes a bigger circle, while using less rope makes a smaller one.
The ability to divide up a length or area with precision was incredibly important to these builders. When working on a piece of paper, a small error does not seem significant. We don't have to worry too much if something does not completely line up. But make that geometric figure larger, and it could cause any structure based upon it to topple. Therefore, the construction given within the previous section is also sometimes known as "The Sand Reckoner's Diagram" for its reliability within these types of building situations.
Funnily enough, the word "Geometry" literally means "Earth measure". The ancients had a deep understanding of mathematics and used some brilliant techniques for surveying land. For example:
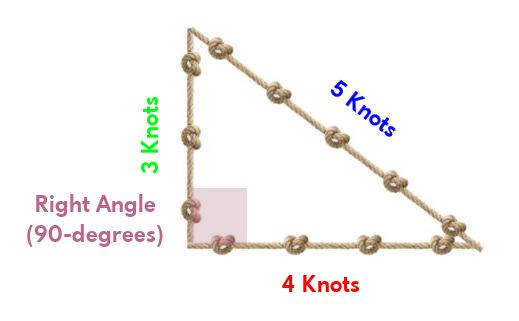
We can take a stretch of rope and tie twelve equally spaced knots within it. If three people pull this rope taught, it makes a special type of right-angled triangle. The "legs" of this triangle have side lengths of three and four knots, while the "hypotenuse" has a side length of five knots (3 + 4 + 5 = 12):
[Image adapted from one at Woodworking Stack Exchange.]
In the same way that we can use basic "Trigonometry" to determine the height of a building without having to measure it, the ancient Egyptians would use this tool to mark out a plot of land without needing to know the length of all of its sides. In short, given an angle and the length of one side, we can determine all of the other properties of a right-angled triangle. These relationships can then be scaled up and down in size, so long as the angles between the sides stays the same.
A similar procedure was used to find the dimensions of various monuments and buildings. There is even a special Egyptian unit of measure called a "Seked" that represents the angle that the face of a pyramid makes vertically. In modern surveying, these types of vertical and horizontal angles are measured with a type of telescope-like device called a "theodolite". Since the ancient Egyptians did not have this type of equipment, what did they use?
"The Pyramid Complex" on the Giza Plateau has three main pyramids. From largest-to-smallest, they are: "The Great Pyramid", "The Pyramid of Chephren", and "The Pyramid of Menkaure". When attempting to tackle the problem of how exactly the Egyptians might have made a survey of the land at Giza before attempting to build The Pyramid Complex, Crichton Miller could not think of an instrument other than a theodolite that would allow them to take precise enough measurements to be able to. He eventually came up with an idea after being inspired by the shape of "The Celtic Cross".
A picture of a Celtic Cross [from Crichton Miller's website]
To quote a nice introductory article by him:
Through intensive and exhaustive experimentation, a belief in the intelligence of our ancestors and a refusal to believe in little green men as the designers, I discovered that the only appropriate instrument that could have been used by the architect, in the place of a theodolite, was a derivative of the cross, with the addition of a plumbline.
This incredibly simple, yet complex instrument, has the potential to measure angles and inclinations to an accuracy of 1 minute of arc or 1/60th of a degree, depending on the size of the instrument used. This is an extraordinary accuracy for what appears to be only two pieces of wood, a scale and a plumbline. One of the most interesting but obscure abilities of the Cross is its capability to take sidereal measurements. [Note: By "sidereal measurements" he means that they were able to pin-point the specific location of objects in the sky, such as the position of a planet at a certain time.]
Some archeological evidence was discovered within The Great Pyramid that seems to indicate that a similar device might have been used during its construction! This was eventually dubbed "The Cross of Thoth", after the Egyptian god "Thoth".
The attributes associated with Thoth are interesting to say the least. From Wikipedia:
The ancient Egyptians regarded Thoth as One, self-begotten and self-produced. He was the master of both physical and moral (i.e. divine) law, making proper use of Ma'at. He is credited with making the calculations for the establishment of the heavens, stars, Earth, and everything in them.
This sort of "cosmic knowing" is reflected within the knowledge of the most ancient of Egyptian societies in a way that borders on the miraculous, especially when it comes to mathematics and surveying. To share a series of quotes from Chapter 3, "The Mystery of Egyptian Science", of the book The Secret History of Ancient Egypt by Herbie Brennan [courtesy of this website]:
One of the terms used by the Egyptians to denote their country was To-Mera, which translates as "the land of the mr." The term mr is frequently rendered as "pyramid," interpreting the phrase as "the country of the pyramid." But however appropriate this might seem, it's not entirely accurate. A better translation might be "the country created to a geometric plan."
"Pyramid" is a secondary meaning of mr and a derived one at that. In its prime meaning, the term describes a very special right-angled triangle with remaining angles of 36 and 54 degrees. The Egyptians used the triangle to generate trigonometric functions.
This startling discovery was made by an Italian Professor of Ancient History, Livio Catulla Stecchini, who specializes in the history of measurement and quantitative science. His specialty, which involves a great deal of mathematical calculation, is opaque to most Egyptologists - indeed to most academics generally - which may be why so many of them have ignored his findings. This is a pity, since his findings have not stopped at Egyptian trigonometry. He has also discovered that Egypt's buildings and cities were laid out according to a deliberate - and elaborate - geometric plan.
[...]
Quoted from Stecchini's paper "Notes on the Relation of Ancient Measures & the Great Pyramid":
"The Egyptians were proud that their country had some unique geographic features which could be expressed in rigorous geometric terms and had a shape which related to the order of the cosmos as they saw it. They believed that when the gods created the cosmos, they began by building Egypt and, having created it perfect, modeled the rest around it."
[...]
Stecchini's use of the term gods is deceptive. According to both the Egyptian priest historian Manetho (writing between 305 and 282 BC) and the Turin Papyrus (compiled between 1279 and 1213 BC), the original founders of Egypt were considered deities. But their cultural descendants, the pharaohs, were also believed to be deities, suggesting that the founders may have been as human as anybody else, despite their exalted reputations. The belief that they created Egypt "perfect" is, however, no myth.
From what we know of Egypt in historical times, the entire country shows signs of having been pre-planned.
[...]
Although conventional Egyptologists deny it (as indicating scientific knowledge far too advanced), Stecchini found proof that the Egyptians used degrees of latitude in their geographical measurements. Their standard unit was 6 minutes or 1/10 of a degree. Unless this was one of the most of the astounding coincidences of the ancient world, it means they were capable of recognizing and accurately analyzing the curvature of the Earth (since you cannot accurately calculate degrees of latitude without doing so). They developed a geographic cubit and used it to measure the total length of their country (1,800,000 geographical cubits) with astonishing accuracy. From this unit they subsequently derived the more familiar royal cubit of approximately 46 cm (18 inches).
Such units were never arbitrary. They had real meaning in relation to the dimensions of the country or the planet as a whole. For example, a convenient unit for measuring large distances was the atur (equivalent, as Stecchini discovered, to 15,000 geographic cubits). This measurement allowed them to calculate the arc of the meridian - a measurement of longitude - more conveniently and accurately than we do today.
[...]
Stecchini is a dense writer, even where his text is free of calculation. But, though ignored by Egyptologists, his fundamental findings can be expressed easily enough: from the very beginning of their history, the Ancient Egyptians possessed advanced geographical understanding - including a knowledge of longitude, latitude and the shape and dimensions of the planet - which enabled them to site their most important cities and monuments in strict accordance with the principles of what they believed to be a sacred science...
Their knowledge of their own country was nothing short of astounding. Stecchini points out that measurements reported by Herodotus, long dismissed (without checking) by scholars as "impossible," turned out, when he examined them, to be wholly accurate. The Egyptians had measured and plotted the location of every major geographical feature from the equator to the Mediterranean.
The sophistication of their approach is seen in the fact that they used three different figures for the Tropic of Cancer. They recorded a precise calculation of 23 degrees 51 minutes, but had a simplified figure of 24 degrees for every day use. Amazingly, they also developed an abstract figure of 24 degrees 6 minutes which enabled them to make accurate observations of the sun's shadow at the summer solstice.
[...]
The point of all this is not that the Egyptian system was sophisticated - which it was - but that its development must have taken centuries and its application millennia. Since the results were already in place in earliest dynastic times...implies the existence of a highly developed culture before the dawn of Egyptian history as we know it.
Are the earliest Egyptian civilizations actually much older than we think? While it is considered a "fringe" idea, some researchers (like the late John Anthony West) claim that the erosion that appears on The Sphinx is due to rainfall that occurred over a long period of time. This would place its creation significantly earlier, around 4,000 years or more before the commonly accepted date.
Plato, the well-known Greek philosopher, gives a brief description of an advanced pre-historical civilization named "Atlantis" within his work Timaeus. While it is usually thought of as a piece of fiction, this information is said to have been relayed to Plato by a Greek statesman named Solon. According to the story, Solon learned this bit of history from an elder Egyptian priest named Sonchis of Sais during his travels in Egypt. Sonchis also told him that the civilization of Atlantis was some 9,000 years before his time! Some claim that Plato's descriptions of Atlantis correspond to "The Richat Structure" in West Africa.
Whatever the case may be, it is certainly intriguing. Were there advanced societies operating long before recorded history? Rather than discovering anew, are we simply recovering what is now lost? There is a lot more that could be said about this topic, but we will save that for another time.
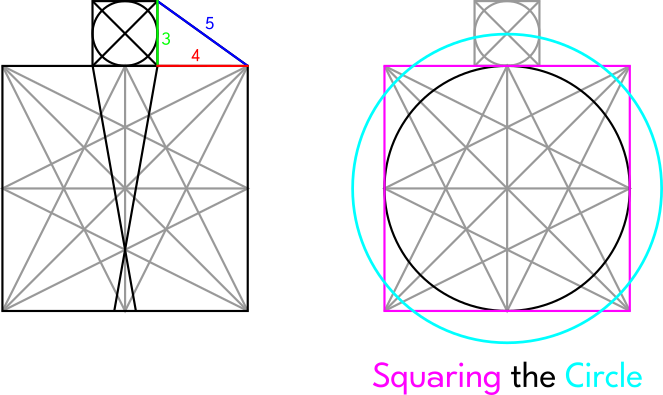
Squaring The Circle
"Squaring The Circle" is to make a square with the same area as a circle. We have covered a little bit of the symbolism behind this figure on another page, but here we want to relate it to the diagrams that we have seen so far.
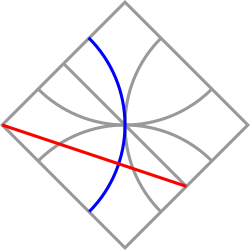
There are actually a few different ways to Square the Circle with enough accuracy to be useful for building. For example, as the researcher Jan Willem Bakker points out, The Sacred Cut square has this property:
The blue arc is nearly the same length as the red line.
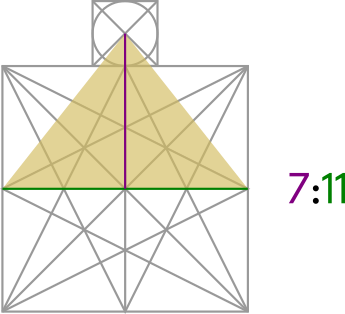
We can also Square the Circle with the division into eleven parts that we did with The Brunés Star:
This is where it gets interesting. If we make diagonal lines from the center of the small circle to the midpoints of the left and right sides of the larger square, then we get the proportions of The Great Pyramid (i.e.: a base of 11 units to a height of 7 units):
This also shows up in Nature...
John Michell noticed that the large and small circles correspond to the dimensions of the Earth and Moon, while John Martineau noticed that the nested circles correspond to the dimensions of the double rainbow:
Photo Credit: Michael S. Schneider
It is the union of Mother Earth and Father Sky!