Back • Return Home
Penta-Psalms
• Basic Pentagon
• The Lute of Pythagoras
• The Fibonacci Star & The Nautical Star
• Basic Decagon
• Schläfli Symbols & Decagrams
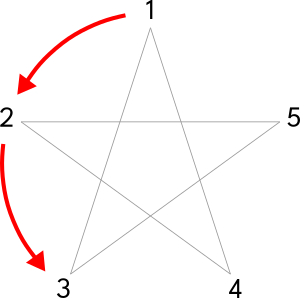
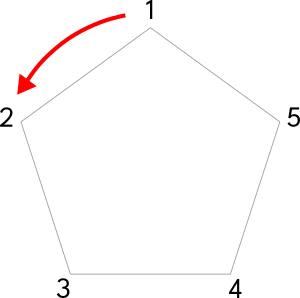
Basic Pentagon (5-Sided Shape)
[Note: These instructions are adapted from those given on pg. 17 of the book Mathographics by Robert Dixon.]
The prefix "penta-" means "five", while the suffix "-gon" means "angle". Thus, a "pentagon" is a shape with five angles.
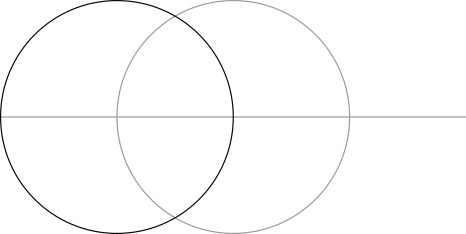
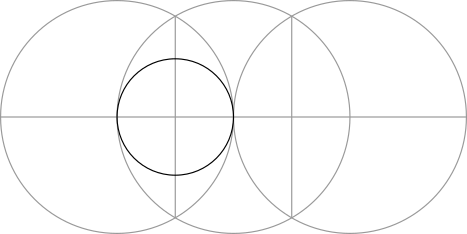
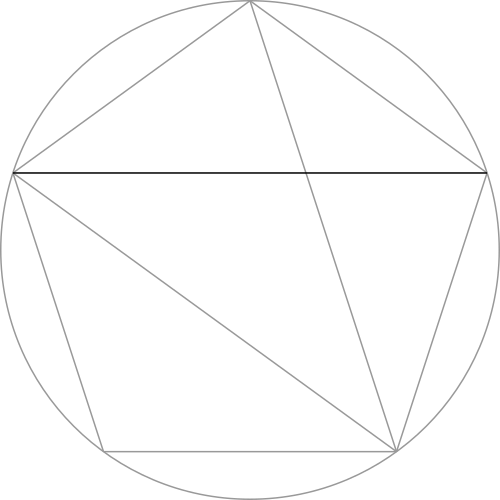
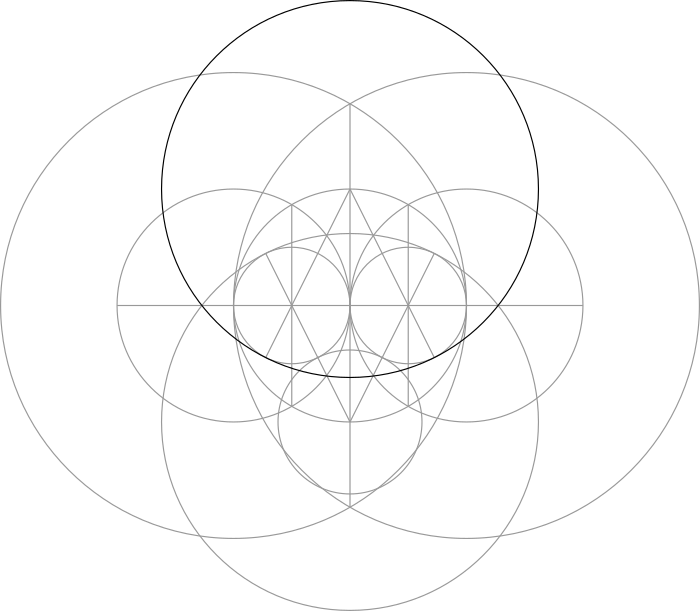
Step 1: Draw a horizontal line and place a circle upon it.
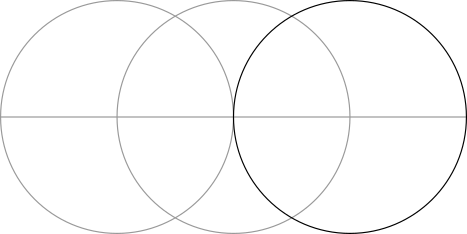
Step 2: Use the points where the circle crosses the line to make two more circles of the same size.
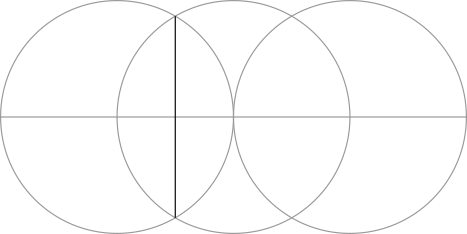
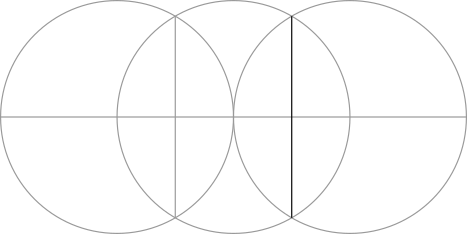
Step 3: Use the points formed by the overlapping circles to make two vertical lines.
Step 4: Use the points formed in the previous step to make two circles.
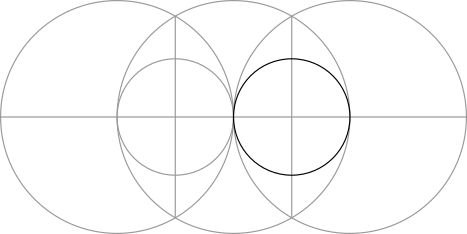
Step 5: Make two larger circles around those formed in Step 2.
Step 6: Use the points where these two circles overlap to make a vertical line that divides the central circle in half.
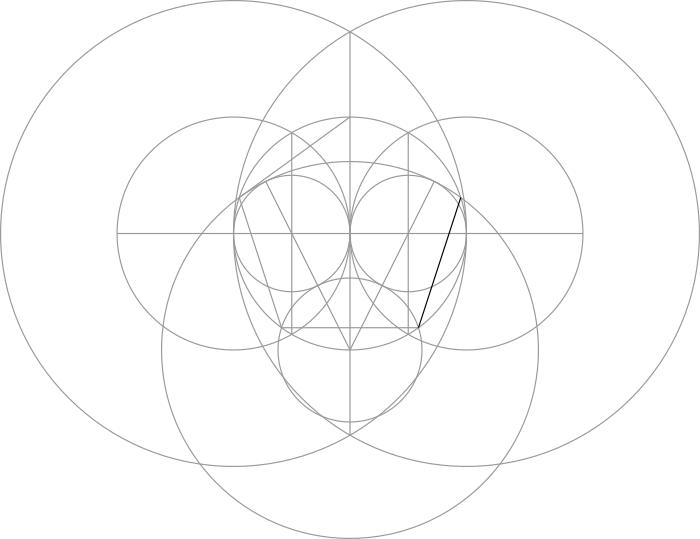
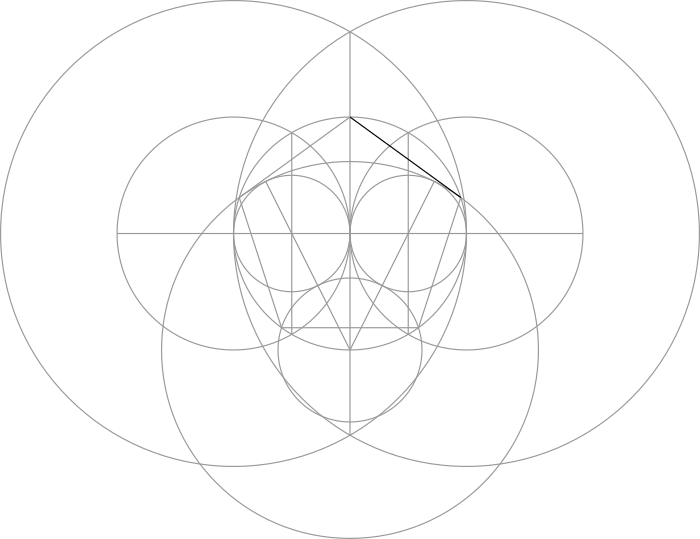
Step 7: Draw a line from where this vertical line crosses the central circle through the center of either of the smaller circles formed in Step 4. Extend the line until it touches the circumference of that smaller circle.
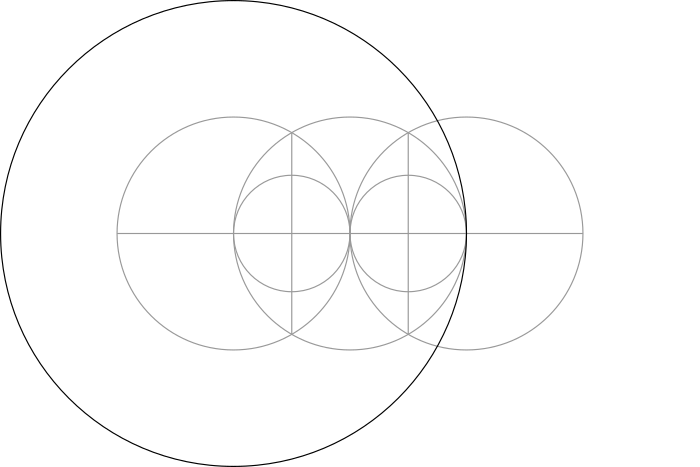
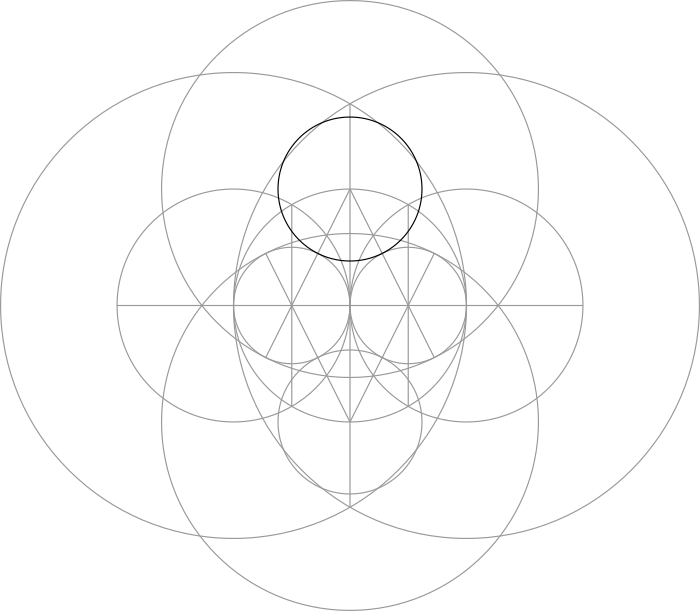
Step 8: Use one of the lines made in the previous step as the radius of a large circle.
Step 9: Use the same line to draw a smaller circle that is tangent to the two circles made in Step 4.
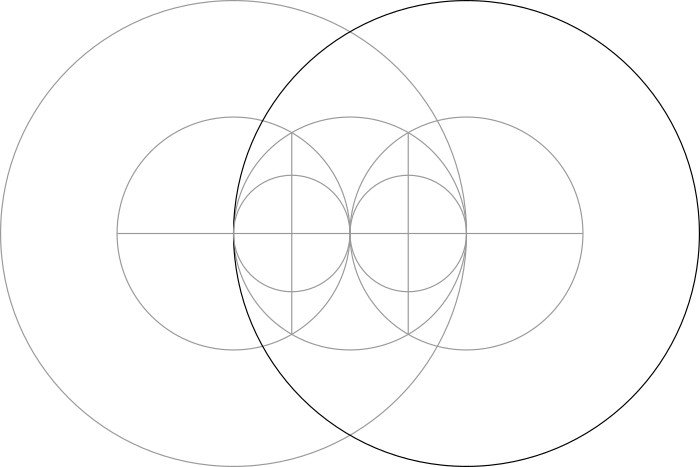
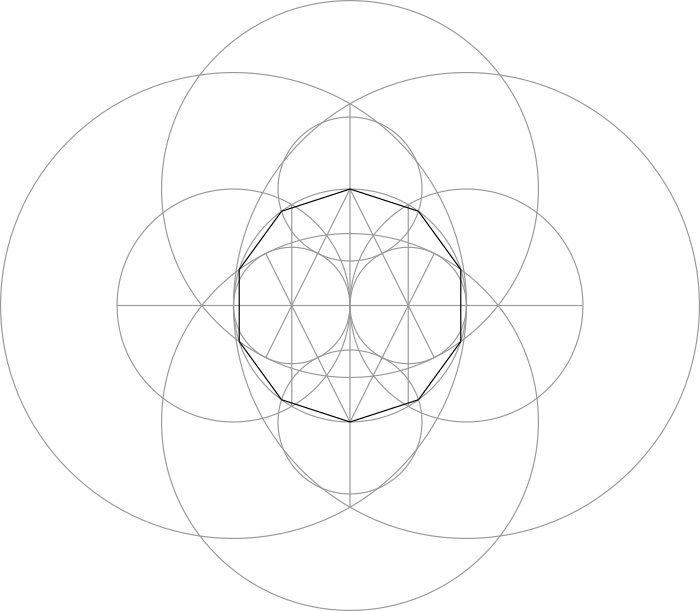
Step 10: The large circle made in Step 8 and the small circle made in Step 9 overlap the central circle at four points. In combination with the vertical line made in Step 6, we can connect them together to form a pentagon.
The Lute of Pythagoras
[Note: These instructions are adapated from the ones given within this document by Ray Fox.]
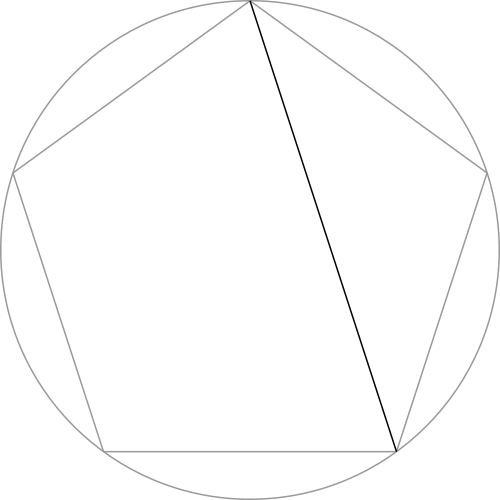
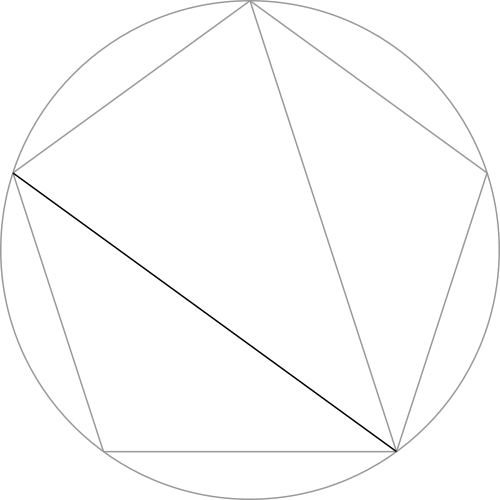
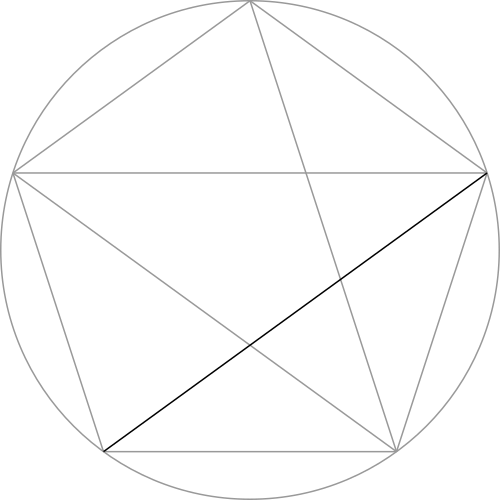
Let's focus in on just the pentagon...
Step 1: Connect together the corners of the pentagon to form a pentagram (i.e.: a 5-pointed star).
Step 2: Connect together the points of the pentagon within the pentagram to make another, smaller pentagram.
Step 3: Use the points on the smaller pentagram to form two small circles.
Step 4: Two points are created by the circles made in the previous step and the point of the larger pentagram. Connect them together with a line.
Step 5: The line made in the previous step forms another pentagon. Connect together the corners of this pentagon to form another, even smaller pentagram.
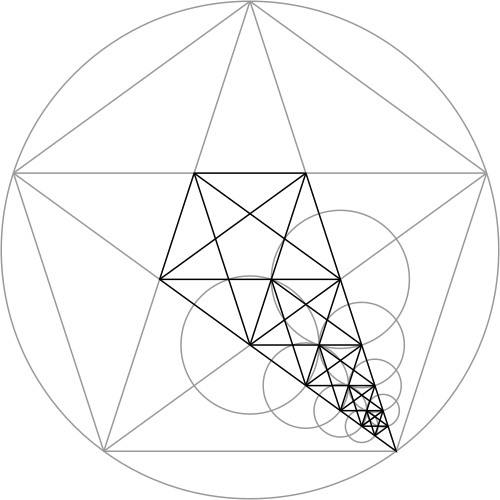
We can repeat this process down the length of the pentagram.
This construction is referred to as "The Lute of Pythagoras".
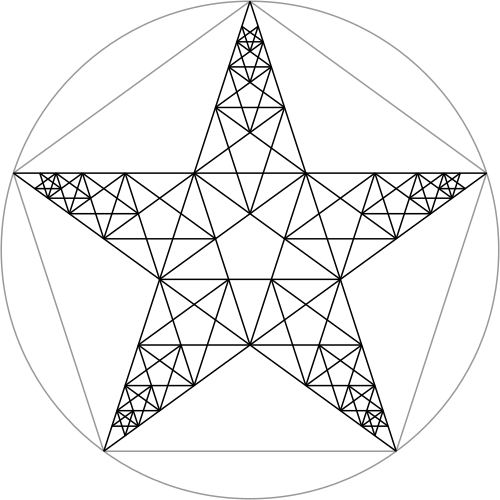
The Fibonacci Star & The Nautical Star
[Note: These instructions are adapted from those given on pg. 131 of the book Patterns In Space by Robert Stanley Beard.]
If we repeat the previous construction within all five points of the pentagram, we get a "Fibonacci Star":
By connecting the tips of a pentagram to the corners opposite them, we form a "Nautical Star":
We can make every star within the Fibonacci Star into a Nautical Star:
Not only is it beautiful, there are a lot of interesting patterns inside of it. For example, connecting together the centers of the smaller stars forms a decagon (i.e.: a 10-sided shape):
These relationships can be used to form many different variations.
Basic Decagon (10-Sided Shape)
The prefix "deca-" means "ten".
This can be thought of as an extension of the Basic Pentagon construction given above. Instead of drawing a pentagon in Step 10, repeat the last few steps at the top of the diagram in addition to the bottom:
This produces ten points around the circumference of the central circle that we can use to draw a decagon:
Schläfli Symbols & Decagrams
There is some useful notation for describing polygons and polygrams. It is called a "Schläfli Symbol". [The name "Schläfli" is pronounced something like "sh-law-flee".] This is how it works...
We can represent a shape with two numbers within wavy brackets and separated by a slash. The first number tells us how many points it has, while the second number (the "winding number") tells us how many points to skip over counter-clockwise in order to draw the next side. So, for example, a pentagram is represented by the Schläfli Symbol {5/2}:
Likewise, a pentagon would be represented by the Schläfli Symbol {5/1} or just {5}:
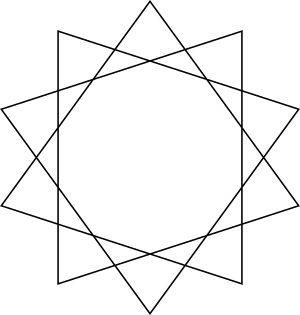
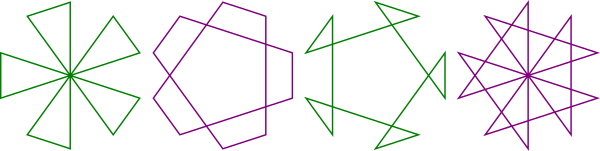
To apply this to decagrams (i.e.: 10-pointed stars), we can make a {10/3}:
This type of star is "unicursal", meaning that it ends at the same point that it begins in a loop.
We can also make a {10/2} or a {10/4} decagram:
This type of star is "compound", meaning that it is made up of multiple polygons or polygrams. In this case, it is a decagram made of two pentagons {10/2} or two pentagrams {10/4}.
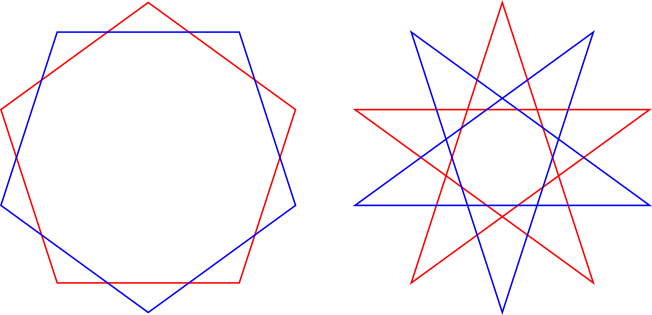
We can also alternate the number of points that we skip in order to make other designs. For example:
While we won't cover these here, we wanted to point out the possibility.