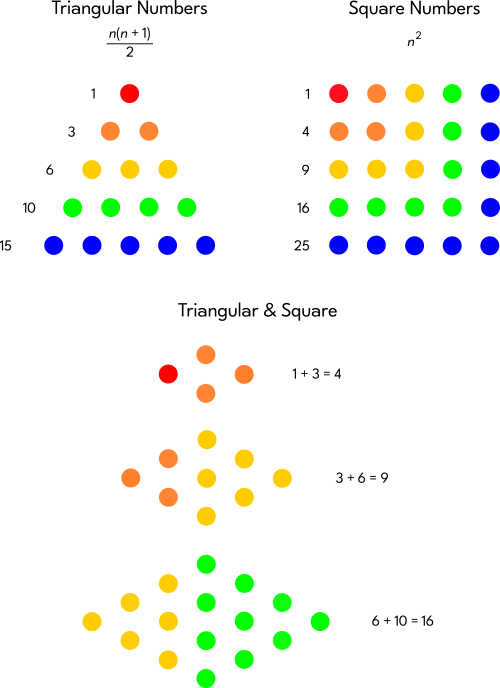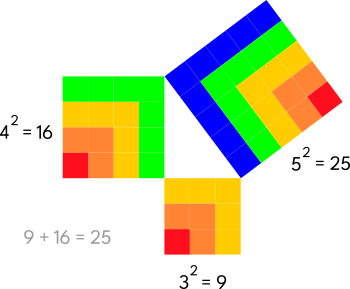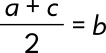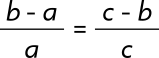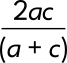Back • Return Home
Pythagorean Number Theory
We spoke briefly about the Pythagoreans before. Here, we will explore different aspects of their mathematics...
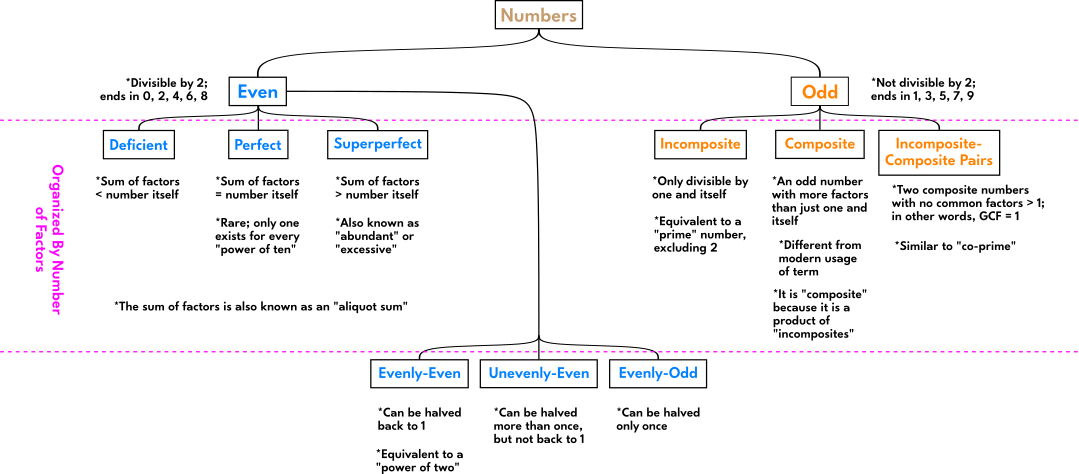
Odd and Even as Male and Female
Evenly-Even = 2n
Sequence:
1, 2, 4, 8, 16, 32, 128, 256, 512, ...
HALVING ↔ DOUBLING
• Property: The sum of terms in the sequence is the next term of that sequence minus 1
Example: 1 + 2 + 4 + 8 = 15, which is 16 - 1
• Property: Pairs of numbers with mirrored positions in the sequence multiply to produce the last number of that sequence; the middle term in a sequence with an Odd Number of terms is multiplied by itself (i.e.: "squared")
Example: 1, 2, 4, 8, 16 → 1 × 16 = 2 × 8 = 4 × 4
Evenly-Odd = 4n + 2
Sequence:
2, 6, 10, 14, 18, 22, ...
These are found by multiplying the Odd Numbers by 2; equivalent to every fourth number from 2...
1 × 2 = 2
3 × 2 = 6
5 × 2 = 10
7 × 2 = 14
9 × 2 = 18
11 × 2 = 22
...etc.
• Property: When each term is divided by an Odd Number, the result is Even, and vice versa.
Example: 18 ÷ 2 = 9 and 18 ÷ 3 = 6
• Property: Each term is half the sum of the two terms next to it.
Example: 6 + 14 = 20 and 20 ÷ 2 = 10
Figurate Numbers
Triangular Numbers: 1, 3, 6, 10, 15, ...
Formed from the sum of consecutive Counting Numbers:
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
...etc.
Square Numbers: 1, 4, 9, 16, 25, ...
Formed from the sum of consecutive Odd Numbers:
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
...etc.
The sum of consecutive Triangular Numbers is a Square Number:
1 + 3 = 4
3 + 6 = 9
6 + 10 = 16
10 + 15 = 25
15 + 21 = 36
...etc.
A "Gnomon" is that part which is added to a shape for it to make a larger copy of itself. It is a process of "self-similarity".
Pythagorean Triples
Ratios & Proportions
The Arithmetic Mean
a < b = b < c
This means that a is less than b the same amount that b is less than c. (They have a "common difference".)
Example: 6:9 = 9:12 (which can also be written as 6:9:12)
Notice that 9 - 6 = 3 and 12 - 9 = 3.
This relationship can also be found with:
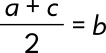
The Geometric Mean
a:b = b:c
Example: 4:6 = 6:9 (which can also be written as 4:6:9)
Notice that 4 is two-thirds of 6 and 6 is two-thirds of 9. (They have a "common ratio".)
This relationship can also be found by multiplying the "means" and "extremes" together. The a and c are "extremes", while the "b's" are "means". Therefore, a × c = b × b.
Example: 4 × 9 = 36 and 6 × 6 = 36
The Harmonic Mean
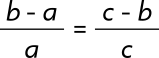
Example: 2:6 = 4:12 (which can also be written as 6:8:12)
Notice that one-third of 6 is 2 and 8 - 2 = 6. Likewise, one-third of 12 is 4 and 12 - 4 = 8.
This relationship can also be found with:
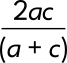
Sequences
To make an Arithmetic Sequence, simply add the same number repeatedly.
Example: 6, 9, 12, 15, 18, 21, 24, etc. [We are repeatedly adding 3.]
To make a Geometric Sequence, simply multiply the same number repeatedly.
Example: 2, 4, 8, 16, 32, 64, 128, etc. [We are repeatedly multiplying by 2.]
To make a Harmonic Sequence, take the Reciprocal of each number in an Arithmetic Sequence.
Example: 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, etc. [We took the Reciprocals of 1, 2, 3, 4, etc.]
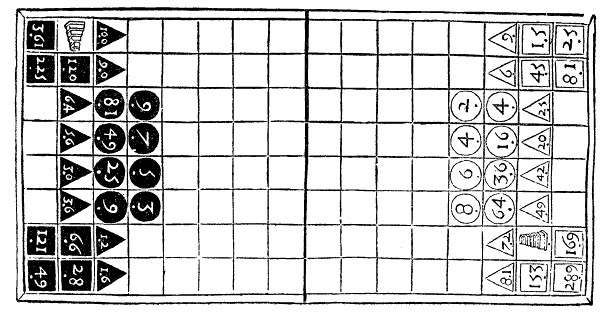
Interestingly, there was a mathematical board game in the Middle Ages that used these sequences as part of its gameplay. It was called "Rithmomachia". It was similar to chess, but each piece had a number on it, and in order to "win" one had to make these kinds of sequences on the other side of the board with their pieces.
A copy of a booklet from the 1500s that describes the rules of this game still exists.
References:
• The section "Pythagorean Mathematics" from the book Secret Teachings of All Ages by Manly P. Hall (which is a summary of Theoretic Arithmetic by Thomas Taylor)
• The 3rd Appendix of the book Skill in Arithmetic by Lawrence Spector
• The section "Aether" from the book Secrets of the Aether by David W. Thomson III
• The article "Harmony and Proportion" by John Boyd-Brent