Let's Learn Together - A Foundation for Chords (Part 1)

Back • Return Home

A Foundation for Chords (Part 1)

This may seem like a lot of information to take in. It is not necessary to memorize any of this to be able to make music, but awareness of these concepts can be helpful sometimes. Please have patience for it. Play around with the ideas as you read. If a section doesn't make sense immediately, skim through it and come back to it later. We will repeat the same concepts in different ways thoughout. Hopefully, it will become more and more clear as we continue on...

Introducing Chords

In the most general sense, "Chords" are just sets of Notes. You might notice that this is the exact same definition that we gave to Scales. Indeed, there is a lot of overlap between the two concepts. However, more often than not, Chords are derived from Scales.

Therefore, when we use the term "Chord", we are usually referring to these smaller sets of Notes within a Scale. Likewise, a "Chord Tone" is a Note inside of a Chord.

When these Chord Tones are all played simultaneously as a single group, then it is called a "Block Chord". We will focus in on Block Chords for now.

Basic Triads

If we take the 1st, 3rd, and 5th Scale Degrees of any Major or minor Scale, then we form a type of Chord. These are called Major and minor Chords, respectively. The 1st Note gives the name of the Chord. This is called the "Root Note". For example, a Chord that comes from the C Major Scale is a C Major Chord and C is its Root. The Notes that make up a Chord are its "spelling". It is often helpful to think of Chords as being like words.

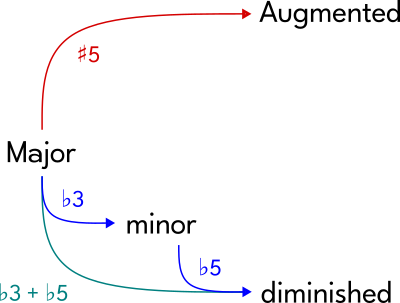
By sharpening or flattening some of the Notes within these Major and minor Chords, we can form two other types of Chords as well: diminished Chords and Augmented Chords.

Here is a table that summarizes a few of the different ways in which we can think of these four types of Chords...

Chord	Major Scale Degrees	Intervals	Half-Step Pattern	General Feeling
Major	1-3-5	M3 + m3 = P5	43	Happy
minor (m)	1-♭3-5	m3 + M3 = P5	34	Sad
diminished (°)	1-♭3-♭5	m3 + m3 = dim5	33	Scary
Augmented (⁺)	1-3-♯5	M3 + M3 = Aug5	44	Mysterious

• The diminished Chord gets its name from the fact that the Interval between the lowest and highest Notes of the Chord is a "diminished 5th" (dim5). Likewise, the Augmented Chord gets its name from the fact that the Interval between the lowest and highest Notes of the Chord is an "Augmented 5th" (Aug5).

• The Scale Degrees are included to emphasize how the Chords are related to Scales. The Intervals are included to demonstrate how all of these Chords are "Tertian" (i.e.: built from a stack of Thirds, whether m3 or M3). Rearranging these Intervals produces other Chords with differing qualities. The Half-Step patterns are included as a way to differentiate the structure of these Chords at a glance (e.g.: notice how both minor and diminished Chords begin with a smaller number of Half-Steps).

Understanding all of these features makes it easy to derive Chords from Scales, to memorize the "spelling" of Chords, and to transform one Chord into another (e.g.: flattening the middle Note of a Major Chord makes a minor Chord, flattening the last Note of a minor Chord makes a diminished Chord, and sharpening the last Note of a Major Chord makes an Augmented Chord).

Any Chord that contains three Chord Tones is sometimes referred to as a "Triad". To reiterate: A Triad is just a Chord with three Notes within it.

It is possible to make Chords with more Notes inside of them, but these basic Major and minor Triads are very important. They will serve as a foundation for a lot of what we will be doing with Chords.

Rearranging A Chord

Generally, a Chord is still the same Chord no matter how we rearrange the Notes inside of it. For example, the C Major Chord is made up of the Notes C, E, and G. And we can play them in the following orders...

C-E-G
E-G-C
G-C-E

All of these are still C Major Chords. However, the order of the Notes within a Chord is important!

If the lowest Note of the Chord is the same as the name of the Chord itself, then that Chord is in "Root Position". The Root Note is on the bottom.

If we take the lowest Note and put it on top of the Chord, then it is called an "Inversion". We have literally "inverted" the Chord by making the lowest Note the highest one instead. The Root Note is now on top. So, to continue our example...

Root Position: C-E-G
1st Inversion: E-G-C
2nd Inversion: G-C-E

The number of Notes within a Chord determines how many Inversions it can have. For example, a Chord with three Notes can only be rearranged twice before we come back to Root Position.

Notice how similar this is to the Inversion of an Interval. This change in Note order also sometimes changes the Intervals inside of a Chord. Remember, Harmonic Intervals occur whenever two Notes are played simultaneously. The quality of the Intervals within a Chord is what determines its sound.

Representing Triads As Roman Numerals

All of the Notes within a Scale can act as a Chord Tone. A Roman numeral shows the Major Scale Degree that a Chord is built from. We can show the type Chord it is by changing the case of the Roman numeral and/or adding extra symbols to it, like this...

• Upper-Case Roman Numerals = Major Chords (sometimes referred to as "Primary Chords")
• Lower-Case Roman Numerals = minor Chords (sometimes referred to as "Secondary Chords")
• Lower-Case Roman Numeral with ° = diminished Chords
• Upper-Case Roman Numeral with ⁺ = Augmented Chords

A ♭ or ♯ in front of the Roman numeral would indicate a Root Note outside of the Scale.

Because all Chords are assumed to be in Root Position, extra numbers are used to describe Inversions. For example:

Root Position	First Inversion	Second Inversion
V	V⁶	V⁶₄

Just to be clear, a "V" would symbolize a Major Chord whose Root is the 5th Degree of the Scale. "V⁶" would symbolize that same Chord in 1st Inversion, and "V⁶₄" would symbolize it within 2nd Inversion.

Chord Progressions

If we play one Chord after another, then it is called a "Chord Progression". Chord Progressions are also sometimes called "Chord Changes" (or just "Changes", for short). For example, the Chord Progression "I → V → vi → IV" is a very simplified, shorthand way of saying:

Play a Major Chord built on the 1st Degree of a Major Scale, followed by a Major Chord built on the 5th Degree of that same Major Scale, followed by a minor Chord built on the 6th Degree of that Major Scale, and finally, end on a Major Chord built on the 4th Degree of that Major Scale.

Whew! That might seem complicated, but it becomes easy once we know the Major and minor Chords well. We will try to make this process as easy as possible.

Functional Harmony

The Harmonic Intervals within our Chords not only determine how the Chords sound, but also how they lead from one into another in the context of a Chord Progression. This is called "Functional Harmony". In short, the "Function" of a Chord is how it wants to move. There are three different types:

• Tonic Function Chords, which produce a sense of resolution or pause
• Dominant Function Chords, which produce a sense of tension or movement
• Subdominant (or "Predominant") Function Chords, which can transition to either tension or resolution

Generally, the more Notes that two Chords share, the closer that they are in Function.

Within every Major Scale we have the following...

• Tonic Function Chords: I, iii, vi
• Subominant Function Chords: IV, ii
• Dominant Function Chords: V, vii°

To trade out one of the Chords within a Chord Progression for another of a similar Function is called a "Chord Substitution".

Harmonic Rhythm

"Harmonic Rhythm" is how fast or slow Chord Changes happen. For example, is there only one Chord per Measure, or several? If the Chord falls on a Beat, it is called "Ictus". When it falls between Beats, it is called "Anacrusis".

Whether a Chord falls on a Beat or between Beats can create either a push or a pull. Therefore, we can control the movement within a piece of music, not only by paying attention to the Function of Chords, but also to the Rhythm in which they are played!