Back • Return Home
Negative Melodies
If we take the Half-Step and Whole-Step pattern between the Notes within every Mode, then we will find that some Modes are reflections of one another:
To reiterate:
Lydian ↔ Locrian
Ionian ↔ Phrygian
Mixolydian ↔ Aeolian
Dorian is its own reflection.
"Music Interval Theory" refers to this phenomenon as "Vertical Reflection". There is also "Horizontal Reflection", which makes the Half-Step and Whole-Step formulas Descending instead of Ascending.
This information is useful for Composing. For example, we can use one Mode for Melodies that are Ascending, and use its reflection for Melodies that are Descending in a "Question and Answer" format.
Negative Harmonies
Let's arrange all twelve Notes of the Chromatic Scale along the circumference of a circle:
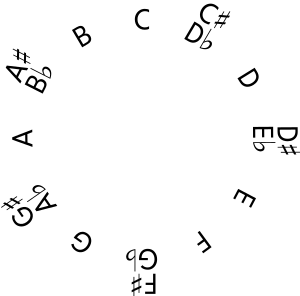
This is called a "Chromatic Circle" or a "Clock Diagram".
Next, pick a Key and a corresponding Chord Progression. For example, we will use the Key of C Ionian (also known as "C Major") and this Chord Progression:
C [C-E-G] → G [G-B-D] → Am [A-C-E] → F [F-A-C]
Draw a line across the entire diagram dividing it in half through the Tonic Note of that Key:

Circle all of the Notes of a particular Chord and see what Notes are within mirrored positions across that line. For example, let's do this with the C Major Chord:
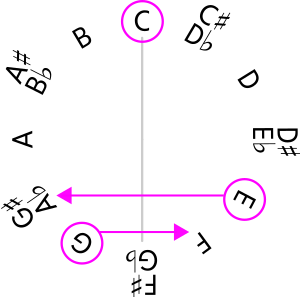
Since we are in the Key of C Major, the C Note of the Chord doesn't move, but the others change. This process gives us another Chord that has a similar Function in relation to the Tonic, but is of a different quality (e.g.: Major Chords become minor and vice versa). [If you are having trouble determining what the new Chord is, there are online tools that might help. For example, this one can identify a Chord from a set of given Notes.]
If we do this for every Chord within our example Chord Progression, then we get the following...
Fm [F-G♯-C] → B♭m [B♭-D♭-F] → A♭ [A♭-C-E♭] → Cm [C-D♯-G]
All of these Chords come from C Phrygian, the reflection of C Ionian.
This information is also useful for Composing. For example, we can use the Chords from both Chord Progressions at the same time to create interesting Cadences.




