Back • Return Home
A Primer On Cubesphere Crystallography
[The following information is based off of the beautiful work of Greg Volk.]
What Is A Cubesphere & How Is It Used?
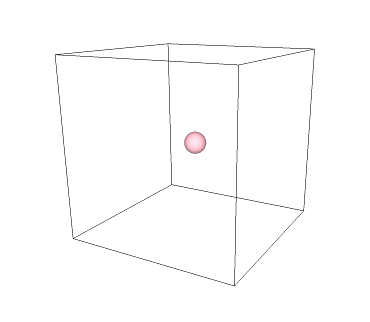
In geometry, the very center of a 3-D form is known as a "centroid". The pink dot in the image below shows the centroid of a cube:
If we make a sphere inside of the cube that shares the same center as it, and then imagine it expanding until it touches as many faces as it can without distorting, we produce an "inscribed sphere" (or "insphere", for short). The golden sphere in the image below shows the insphere of the cube:
If we take both of them together (i.e.: cube + insphere), then we get what Walter and Lao call a Cubesphere. It is just that simple! Now, what else can we do with it?
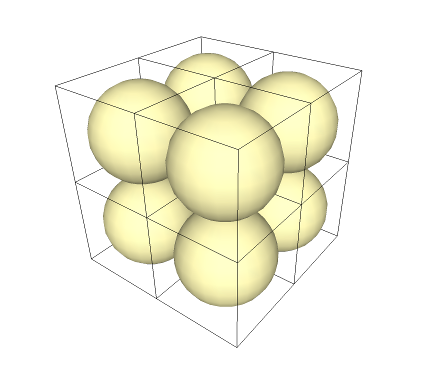
A cube is known as a "space filler", meaning that when you pack cubes together, they can fill space without any gaps. Let's pack together some Cubespheres:
If the spheres were atoms, this would be equivalent to a "cubic crystal system".
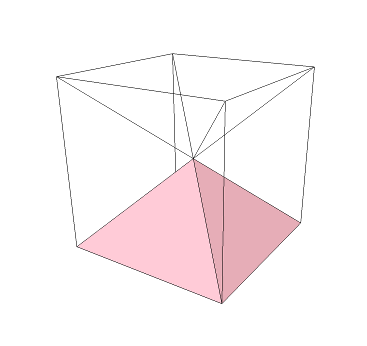
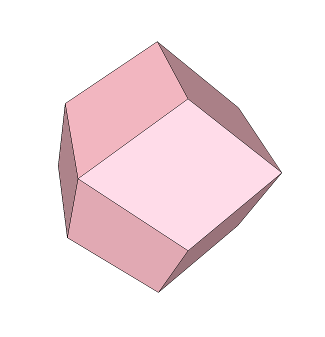
Take a cube and divide it along its diagonals so that we get six "square pyramids" (which are just pyramids with a square base). In the image below, one square pyramid is highlighted in pink:
Take another cube of the same size and match up each square pyramid with each of its faces:
We end up with another shape called a "rhombic dodecahedron":
[Click here for a rotating model of this figure from Wikipedia]
The prefix "do-" means 2, and the prefix "deca-" means 10. The diamond shape of each face is a "rhombus", and there are 12 of them. Hence, "rhombic dodecahedron".
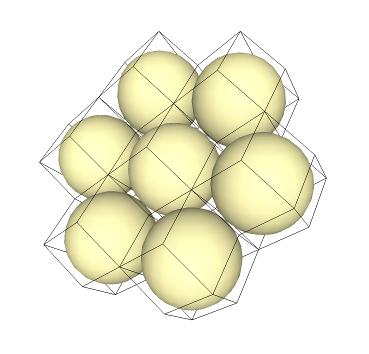
The rhombic dodecahedron is also a space filler! Let's pack them together with their inspheres:
Again, if the spheres were atoms, this would be equivalent to a "hexagonal crystal system".
Here is the important part: By dividing up the cube in various ways and re-arranging them in a manner similar to what we have done above, we can create every type of crystal structure.
From The Home Study Course (1st Edition) - Unit 8:
There are no other forms in Nature than these cube-spheres and sections of them.
How humbling it is to know that one thing can become anything else just by simple rearrangement.
The Importance of Crystals
Everything crystallizes, but the more seemingly complex the system, the more amorphous (or formless) they might seem to be. Let's do some more geometry together...
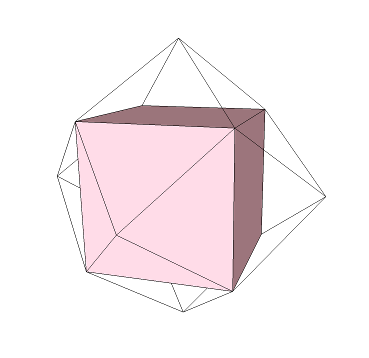
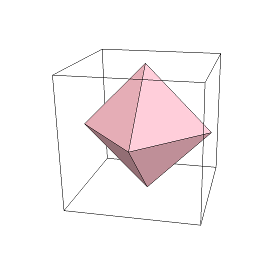
If we connect together the center of each face of the cube, then we get another figure:
This is an "octahedron". The prefix "octa-" means 8, and the suffix "-hedron" means "face". Therefore, an "octahedron" has 8 faces.
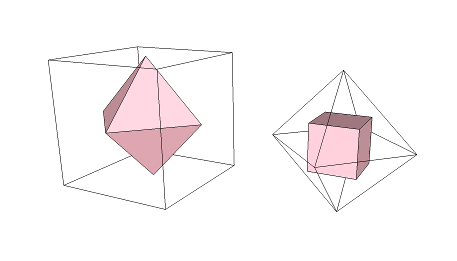
Whenever we turn faces into "vertices" (or corners) in this way, we get the "dual" of a shape. The cube and octahedron are "duals" of one another:
Each can become the other.
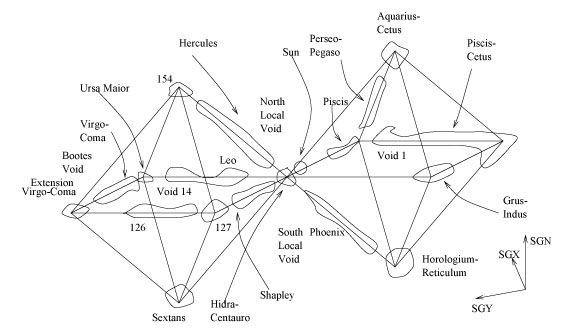
Galaxies can make groups called "superclusters". Like a kind of macroscopic molecule, these too have crystal structures. The superclusters which are next to the galaxy that we are in, the Milky Way, form octahedral shapes!
Image from Large Scale Structure & Magnetic Fields by E. Battaner & E. Florido
Space Geometry indeed!
Here are a couple of Walter's drawings that demonstrate the same kinds of patterns: