Back • Return Home
Mapping Out Space and Time With Magic Squares
Abstract: As Geonometry repeatedly demonstrates, magic squares have direct application to fundamental Physics. However, is there some basis for this within more "traditional" mathematics and science? Please feel free to gloss over whatever aspects of this article might seem overly complex.
A fantastic summary of the traditional view of magic squares is given within the 1993 paper Matrix Properties of Magic Squares by Daryl Lynn Stevens.
However, this paper also culminates in an understanding that gets us closer to how magic squares can be used within the context of Physics (by relating them to "matrices" and "vector spaces"). Some more recent work that covers this topic in-depth is that of Peter Loly. To quote the 2006 article Magic Square Physics by Ivars Peterson from ScienceNews [with some extra highlighting by me]:
The study of magic squares has a long, long history. In ancient Babylonian times, these array of numbers were held to have magical powers. Over the years, they have also served as protective charms and religious symbols.
At the recreational level, they're fun for all ages, says Peter Loly of the University of Manitoba.
Loly himself has investigated the "physical" properties of magic squares - treating the numbers of each such square as physical quantities.
A magic square is a square matrix drawn as a grid filled with numbers. It consists of a set of integers arranged in the form of square so that the numbers in each row, column, and diagonal all add up to the same total. If the integers are consecutive numbers from 1 to n2, the square is said to be of nth order. The magic sum itself is given by n(n2 + 1)/2.
Suppose, for example, you interpret the numbers as masses. You can then determine a magic square’s moment of inertia about a given axis of rotation. For any specific case, you obtain the moment of inertia, In, of a magic square of order n about an axis at right angles to its center by summing mr2 for each cell, where m is the number centered in a cell and r is the distance of the center of that cell from the center of the square measured in units of the nearest neighbor distance.
You find that the moment of inertia, Iz, about the square's center (an axis at right angles to the square) is twice the moment of inertia about an axis of rotation along the center row or column.
In general, you can show that, for order n, Iz = [n2 + (n4 – 1)]/12.
So, for n = 3, Iz = 60; for n = 4, Iz = 340.
"This is the only property of magic squares, aside from the line sums, which is solely dependent on the order of the square, n," Loly and Adam Rogers note in a paper published in 2004 in the Canadian Undergraduate Physics Journal.
The same formula applies to semi-magic squares, which don’t meet the standard requirement that diagonals also sum to the magic number.
Such an analysis can be extended to magic cubes. A magic cube consists of n3 numbers, arranged so that each row, column, and main diagonal give the same sum. In the case, the magic constant is n(n3 + 1)/2.
Here's one example.
The three layers (above) of a 3-by-3 magic cube.
Loly and Rogers show that the moment of inertia of a magic cube is n3(n3 + 1)(n2 – 1)/12. In effect, they demonstrate that magic cubes have the same inertial form as a spherical top.
It's also possible to consider the numbers of magic squares to be electric charges and to extend such analyses to higher dimensions. Loly has even calculated the so-called eigenvalues of magic squares, which are related to their "fundamental frequencies" if you were to set these squares ringing like a bell.
"When treated as mass distributions, magic squares give clear and accessible examples of the properties of the moment of inertia," Loly says. "When treated as matrices, magic squares also serve as exceptional examples of some advanced linear algebra theorems."
In a similar manner, Peyman Fahimi and Babak Jaleh describe the electrostatic potential of a magic square when each of the numbers is treated as a point mass. While several mathematicians have noted how magic squares can be used in creative ways to teach specific branches of mathematics, like Linear Algebra, these types of connections seem to go far beyond mere representation. They hint at an underlying mathematical order to reality...
In some of the other research presented on this website, we have put forth the idea that it is possible to create a one-to-one correspondence between numbers and physical objects to such an extent that mathematical patterns within those numbers can yield a deeper understanding of the objects themselves. The line between pure mathematics and physical observation starts to blur.
The work of Craig Knecht provides a very striking example that can be readily sensed. To quote the webpage Magic Square Models on Harvey Heinz's Recreational Math website:
A three-dimensional magic square
The idea for this novel magic square was sent to me by Craig Knecht on June 5, 2001.
| 25 |
11 |
2 |
8 |
19 |
| 3 |
9 |
20 |
21 |
12 |
| 16 |
22 |
13 |
4 |
10 |
| 14 |
5 |
6 |
17 |
23 |
| 7 |
18 |
24 |
15 |
1 |
This is an order-5 pandiagonal associated magic square. The numbers in each cell are represented by metal washers. In this picture, the model is suspended from the ceiling to illustrate the balanced nature of all magic squares.
The 325 metal washers give this model a weight of almost 2 pounds.
One is inclined to ask why the numbers in the magic square distribute the weight of the washers in this manner.
We've already mentioned how the patterns within magic squares could relate to abstract particles. What about larger atoms and molecules? Can we move from describing fundamental Physics into the Chemistry and Biology essential to life? I will offer some conjecture here...
Craig Knecht has also done some incredible work that relates magic squares to a particular type of geometry known as a "space-filling curve". To quote the 2016 article Magic Space by Greg Ross from the Futility Closet blog:
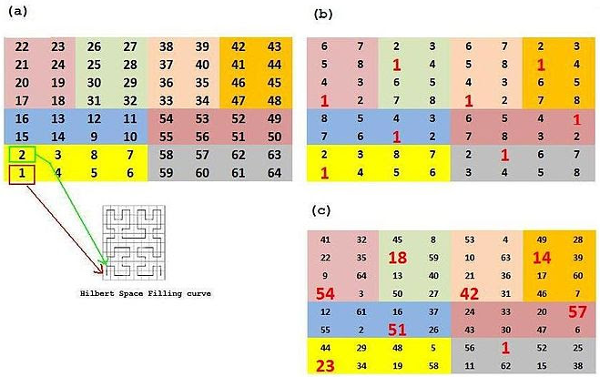
Craig Knecht, whose "terraformed" magic squares we explored in 2013, has begun to experiment with applying "magic" properties to David Hilbert's space-filling curve.
The Hilbert curve finds its way to every cell in the square above by following the pattern shown at the lower left. Knecht divided that path into eight-cell segments, as shown in (a), and then sought solutions in which each colored eight-cell panel produced the magic sum of 260 while each of the eight ordinal positions across the eight panels did so as well. For example, in (b), a large red digit 1 marks the "first" position in each panel; the hope was to find values for these eight cells that would sum to 260, and likewise for all the "second" cells, the "third" ones, and so on.
The result, shown in (c), is a "most-perfect" magic square: Each colored panel sums to 260, and every set of cells that are 8 spaces apart on the Hilbert curve also sum to 260.
The next step was to apply this idea in three dimensions, and recently Knecht made the breakthrough shown below - a 4×4×4 "most perfect" number cube. The 64 numbers in the cube can be broken into 36 2×2 subsquares in each dimension, as shown. In all 108 of these subsquares, the four constituent numbers total 130. And as with the two-dimensional square above, a Hilbert curve can be drawn through the cube that visits each cell once, and cells that are eight cells apart on this curve sum to 260.
One of Knecht's correspondents pointed out that the cube is even magicker than he had supposed: The "wraparound" subsquares (for example, 5, 28, 44, and 53 on the top of the cube) also sum to 130, as does each set of four corners, making a total of 192 2×2 subsquares that sum to 130.
"So in summary ... making the Hilbert space-filling curve path have this magic property of values 8 spaces summing to the magic constant + this 2×2 planar criteria produces a very interesting cube!"
The numbers involved are not arbitrary. For example, why 260? It is a number that seems to show up in some interesting places. To quote the article The Fibonacci Numbers: Connections within the Mathematics and Calendrical Systems of Ancient Mesoamerica by Valerie Vaughan:
The Mesoamericans, like all civilized peoples of the world, developed and abided by a calendar based on the approximate length of the tropical year (365 days). But they also used a second calendar unlike any other in the world. Known variously as the tzolkin (Yucatec) or tonalpohaulli (Nahuatl), it was 260 days in length, and served as an astrological almanac or sacred calendar for all peoples of ancient Mesoamerica. It is even still in use today in some parts of Mexico and Guatemala. This calendar guided the daily rituals and cultural achievement of the people, but it also formed the basis for interconnecting the various measurements of cyclical time.
Despite the importance of the 260-day calendar for ancient Mesoamericans, no explanation has been generally accepted as to how, why, or exactly where this time-keeping method began. [...]
The fact is that the ancient Maya discovered a mathemagical key that linked nearly every known astronomical cycle. With the number 260 and its component divisors (13 × 20, 5 × 52, etc.), they could interconnect all the apparent time sequences of observable celestial cycles -- solar, lunar, eclipse, Venus, Mars, Mercury, even the cycle of precession. The 260-day calendar was used to denote multiple interrelated systems; for example, it could be brought into phase with the 365-day calendar once every 52 years, which was an important cycle for the Maya. This period of 52 years is called the Calendar Round, the hunab (Maya) or xiuhmolpilli (Nahautl).
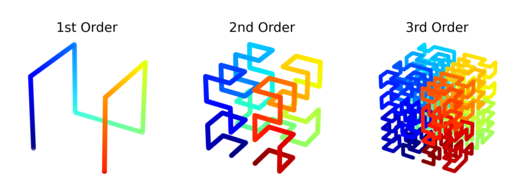
The geometry does not seem arbitrary either. There is a way to connect multiple copies of a Hilbert curve back onto itself to form a loop. This is known as a "Moore curve". Can we do something similar with the magic cube shown above?
A 3-D Moore curve taken from the previously linked page.
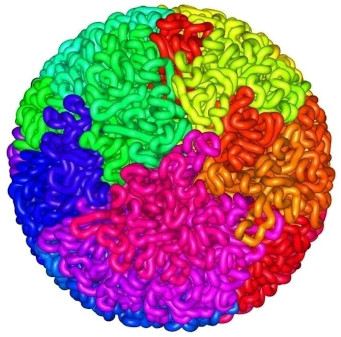
Because it has to be able to unwind without becoming tangled, the way that DNA packs into the nucleus of a cell follows a similar space-filling curve...
Image from the article: The Mystery of the Instant Noodle Chromosomes @ PysOrg
Image from the article: 3-D Image Shows How DNA Packs Itself into a "Fractal Globule" @ SciTechDaily
Fascinating stuff! ☺