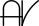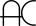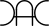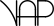Back • Return Home

The Classification of Number

Before we go too deeply into the Syndex system, we must first understand some more simple terminology, most of which is from the branch of Mathematics called "Number Theory". Number Theory is the study of the properties of numbers and the various groups that they can be classified into. We will try to make all of this as simple as possible...

Contents

• Basic Types of Number & Their Properties
• Two-Way Motion
• The 12 Archetypal Number Classes
• In Summary

Basic Types of Number & Their Properties

Term Definition
Multiple "Multiples" are all of the whole numbers formed when any number is multiplied repeatedly. For example, 10, 15, 20, 25, and so on, are all "multiples" of 5. In this case, it is like "skip counting" by fives.
Factor "Factors" are all of the whole numbers by which another number can be divided into without remainders. It is thus "divisible" by that number. For example, 3 and 5 are "factors" of 15 because 15 ÷ 3 = 5 and 15 ÷ 5 = 3. So, 15 is divisible by both 5 and 3.
Even Numbers "Even Numbers" are all of the whole numbers that are divisible by 2. The last digit of such numerals is always 0, 2, 4, 6, or 8.
Odd Numbers "Odd Numbers" are all of the whole numbers that are not divisible by 2. The last digit of such numerals is always 1, 3, 5, 7, or 9.
Perfect Numbers "Perfect Numbers" are all whole numbers whose factors add together to form that number. For example, 6 is the first perfect number because:

6 is divisible by 1, 2, and 3
and
1 + 2 + 3 = 6

In Syndex, the following three types of numbers can be represented by their own special symbol:

Glyphs Meaning
"Square Numbers" are the whole numbers formed by multiplying a whole number by itself. This is symbolized by a small number 2 to the upper right called an "exponent". For example:

12 = 1 × 1 = 1,
22 = 2 × 2 = 4,
32 = 3 × 3 = 9,
etc.

Therefore, the numbers 1, 4, and 9 are "Squares".
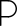"Prime Numbers" are the whole numbers that only have factors of themselves and 1. They can't be divided into equal groups by any other whole number. For example, some of the smallest "Primes" are 2, 3, 5, 7, 11, 13, etc. Other than the number 2, they are always an odd number.
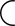"Composite Numbers" are the whole numbers that have more factors than just themselves and 1. They can be thought of as almost like the opposite of a Prime, but they can be either even or odd. For example, 12 is "Composite" because it has many factors (1, 2, 3, 4, 6, and 12).

There are also "Highly Composite Numbers", which are the whole numbers that have more factors than any number coming before them. For example, the first few Highly Composite Numbers are 1, 2, 4, 6, 12, 24, 36, 48, 60, etc.

There is a lot more that could be said about all of these types of numbers, but we only need to cover them in a general manner here. Now, let's explore how Syndex uses them...

Two-Way Motion

Any type of forward motion is referred to as Progressive or Graduating. Conversely, any type of backward motion is referred to as Regressive or Retrograde. We might think of numbers as only existing in a linear sequence, increasing or decreasing one at a time. In actuality, numbers have Ambidirectional Reflexivity. Let's break this word down. Ambidirectional is when something moves in two directions simultaneously, while Reflexivity is when a thing is self-referencing, bending back in on itself. We can begin to see the backwards moving patterns in numbers by reversing the digits within any multi-digit numeral. This operation of "mirroring" is given its own special symbol:

Glyph Meaning
This is the symbol for mirroring, or Retrocity. It looks like a stylized letter "A", or perhaps an upside-down letter "U" with a line through it.

This operation allows numbers to take on three different characteristics:

Term Definition
Palindromic A "palindrome" is something that is the same forwards and backwards. The number itself does not change when mirrored. These are also sometimes referred to as Binomial Reflection Numbers.
Transpalindromic The prefix "trans~" means "beyond, across, or through". Therefore, this name literally means something like "this number's properties are beyond mirroring". In other words, while the number itself changes, the type of number it is does not. These are also sometimes referred to as Transbinomial Reflection Numbers.
Retro~ The prefix "retro~" means "backward, reverse". Therefore, the properties of any type of number which has this prefix appended to its name, will change when mirrored.

Thus, each of the Prime, Composite, and Square Numbers can also be classified as Retro~, Palindromic, or Transpalindromic in form. This gives rise to twelve distinct groups called Archetypal Number Classes, each of which is represented by its own unique symbol. While this might sound complex, it is actually very easy to understand after one sees a few examples...

The 12 Archetypal Number Classes

Glyphs Meaning
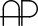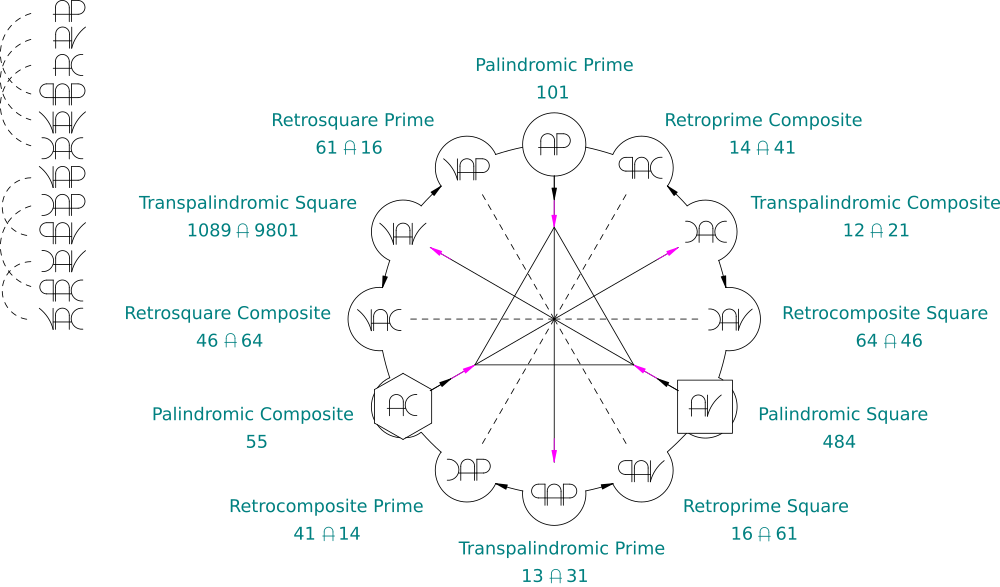
Palindromic Prime - A number that is both Palindromic and Prime. [Example: 101]
Transpalindromic Prime - A number that is Prime both forward and backward. [Example: 13 is Prime, and its mirror, 31, is also Prime.]
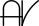Palindromic Square - A number that is both Palindromic and Square. [Example: 484 is 22 × 22]
Transpalindromic Square - A number that is Square both fowards and backwards. [Example: 1089 is 33 × 33, 9801 is 99 × 99, and both are mirrors of one another.]
Palindromic Composite - A number that is both Palindromic and Composite. [Example: 55]
Transpalindromic Composite - A number that stays Composite when mirrored. [Example: 12 is Composite, and 21, its reverse, is also Composite.]
Retrosquare Prime - A number that begins as Prime and becomes Square upon mirroring. [Example: 61 is Prime, while its reversal, 16, is Square, 4 × 4.]
Retroprime Square - A number that begins as Square and becomes Prime upon mirroring. The inverse of the above number class.
Retrocomposite Prime - A number that begins as a Prime number and becomes Composite when reversed. [Example: 41 is Prime, but 14, its mirror, is Composite.]
Retroprime Composite - A number that begins as a Composite but becomes a Prime when mirrored. The inverse of the above number class.
Retrocomposite Square - A number that is a Square and becomes Composite upon mirroring. [Example: 64 is 8 × 8, a Square, and its mirror, 46, is Composite.]
Retrosquare Composite - A number that is Composite and becomes Square upon mirroring. The inverse of the above number class.

While the glyphs are more like mathematical expressions, not acronymns, it is sometimes convenient to type them out as whatever letters that they most resemble. Like this:

Archetypal Number Classes Glyph Looks Like...
Palindromic Prime AP
Transpalindromic Prime PAP
Palindromic Square AV
Transpalindromic Square VAV
Palindromic Composite AC
Transpalindromic Composite CAC
Retrosquare Prime VAP
Retroprime Square PAV
Retrocomposite Prime CAP
Retroprime Composite PAC
Retrocomposite Square CAV
Retrosquare Composite VAC

Unfortunately, however, it removes the helpful mirroring of the first character in the glyph, so we will continue to use the glyphs for the sake of clarity.

All of the above information can be condensed and conveyed through a single diagram:



It is important to note that none of these Archetypal Number Classes can be separated from each other without destroying the coherence of the system as a whole because they function together as one. They mutually define one another. In other words, each of them only make sense in reference to all of the others!

In Summary

There are three types of numbers classified by how many factors they have:

• Primes - Only themselves and 1 are factors.
• Composites - An even number of factors.
• Squares - An odd number of factors, because one of those factors is multiplied by itself.

These can be mirrored in three different ways:

• Retro~ - Becomes a different type of number upon mirroring.
• Palindrome - Is the exact same number both forward and reverse.
• Transpalindromic - Is the same type of number both forward and reverse, even though the number itself changes.

This process forms twelve Archetypal Number Classes:

• Palindromic Prime - A Palindrome number which is Prime.
• Transpalindromic Prime - A number which stays Prime upon mirroring.
• Palindromic Square - A Palindrome number which is Square.
• Transpalindromic Square - A number which stays Square upon mirroring.
• Palindromic Composite - A Palindrome number which is Composite.
• Transpalindromic Composite - A number which stays Composite upon mirroring.
• Retrosquare Prime - A Prime that becomes a Square.
• Retroprime Square - A Square that becomes a Prime.
• Retrocomposite Prime - A Prime that becomes a Composite.
• Retroprime Composite - A Composite that becomes a Prime.
• Retrocomposite Square - A Square that becomes a Composite.
• Retrosquare Composite - A Composite that becomes a Square.

Next Section →