Back • Return Home
An Introduction To The 9-11 Cycloflex Exemplary Basewave
It is important to read the previous two articles, The Fundamentals of Syndex and The Classification of Number, to fully grasp the following. While it may seem complicated, please have patience for it. Feel free to skim sections that do not make sense the first time around, and come back to them again after finishing the article. Try to play around with the patterns described so that they can become more familiar to you. Having a sheet of paper, a pencil, and a simple calculator handy might help.
Contents
• Base-Ten
• Nine and Eleven
• Squares and Primes
• Two New Mathematical Operations
• In Summary
Base-Ten
Most of the time when dealing with number we use what is called "base-ten". This just means that we use ten symbols to represent every quantity:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
We cycle through the same ten symbols over and over again, and every time that we reach a group of ten (such as 10, 100, 1000, etc.), we attach another digit to the right. Therefore, the order of the symbols determines the amount that it represents.
In Syndex, while every numeral is seen as an aspect of a unified system, quantity is interpreted as beginning with 2 (or Binarity). The numerals 0 and 1 (or Singularity) are considered unique. [This is the case in traditional mathematics to some extent as well. For example, 0 is called the "additive identity" because any number plus 0 is the same number. In a sense, that number kept its "identity" and did not change. Likewise, 1 is called the "multiplicative identity" because any number times 1 is the same number. In short, 0 and 1 don't add and multiply like other numbers!]
2 through 9 makes eight distinct base numerals, an "octave" of sorts. (The prefix "oct-" means "eight".) This concept will come up again and again as we continue...
Nine and Eleven
Within base-ten, the operation of Retrocity or mirroring (symbolized by the  glyph) is controlled by the numbers 9 and 11. Notice that 9 is one less than our base, and 11 is one more than our base (i.e.: 10 - 1 = 9 and 10 + 1 = 11).
glyph) is controlled by the numbers 9 and 11. Notice that 9 is one less than our base, and 11 is one more than our base (i.e.: 10 - 1 = 9 and 10 + 1 = 11).
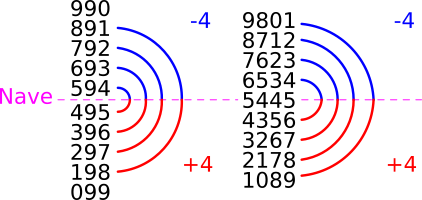
It might be obvious how 11 is related to mirroring (because it is Palindromic), but how does 9 relate to mirroring? If we take multiples of 9, we can readily see the mirroring inherent to 9:
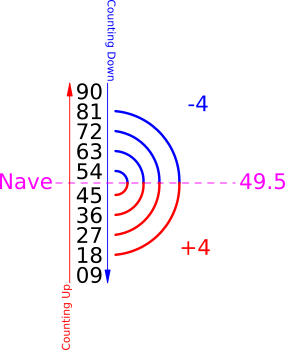
Notice how the numbers are moving in two directions simultaneously (i.e.: the tens place seems to count up, while the ones place seems to count down). They also contain an octave (of 4 forward and 4 reverse) that seems to turn around at 49.5. The term Nave (derived from the word "navel") is the halfway point. It is like a point of inversion, showing that the second half of the pattern is the reverse of the first half. The multiples of 11 have the same Nave:
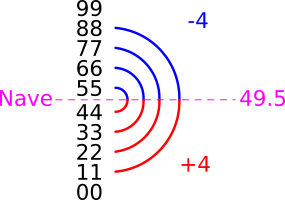
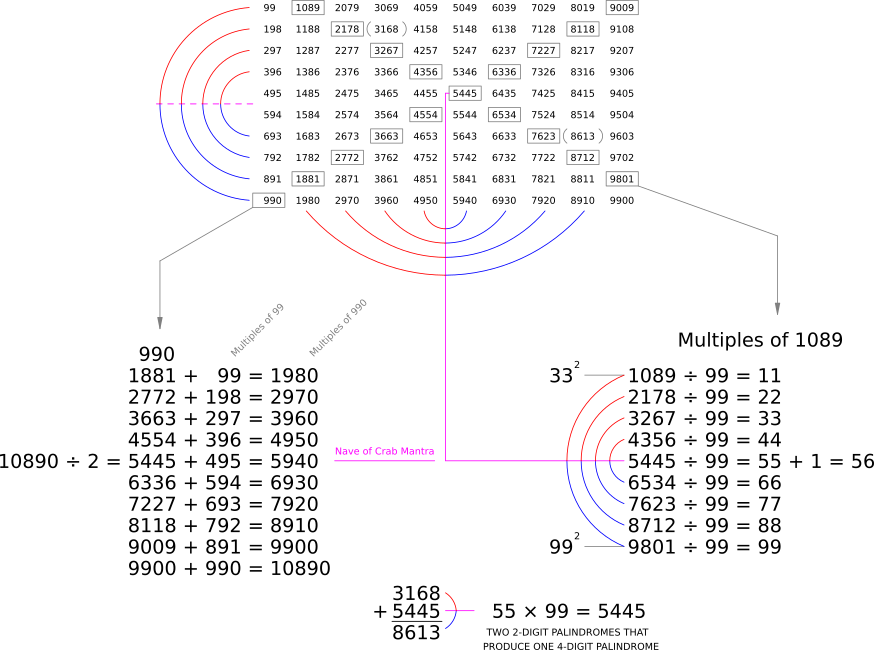
These patterns persist into higher digit numbers when we combine 9 and 11. For example, to see the mirrorings in 3 and 4-digit numbers we can take multiples of 99 (which is 9 × 11) and multiples of 1089 (which is 99 × 11):
This continues up to any number of digits. For example, 5-digit mirrorings are produced with multiples of 10890 (which is 990 × 11), 6-digit mirrorings are produced with multiples of 108900 (which is 9900 × 11), and so on. Robert Marshall sometimes depicts this mirroring quality embodied by 9 and 11 with a crab (probably due to the symmetrical nature of its body shape and how many species of crab walk sideways):

[This little guy is derived from the art piece "Crab" by M.C. Escher.]
A diagram called the Crab Mantra gives us some more detail in how multiples of 99 (arranged in a 10 × 10 grid) can reveal some very intriguing symmetries, showing just how throughly interconnected 9 and 11 are. The "x"-shape within the table is like a crab and the repetition of 99 is its mantra. ☺
While these patterns are beautiful to look at, they also have a deep significance to mathematics as a whole, for they hint at an underlying dynamic permeating the entirety of number itself. This dynamic is called The 9-11 Cycloflex Exemplary Basewave (or The 9-11 Cycloflex for short). To more fully explain the name:
The reflective patterns of 9 and 11 are a perfect example of two-way, wave-like motions throughout the base-ten system (an "Exemplary Basewave"). They appear when we treat numbers as reflexive (i.e.: when we bend the number continuum back upon itself by organizing it into cycles, instead of treating it as something that only unfolds linearly in one direction). Hence, they are also a "Cycloflex" (from a combination of the words "cyclic" and "reflexive").
This might seem complicated, but all that we need to remember is that the mirroring exemplified by 9 and 11 affects the qualities of all other numbers. This is what produces the twelve Archetypal Number Classes. For example, within the Crab Mantra diagram above, we see that 332 = 1089 and 992 = 9801. Each one of these numbers (1089 and 9801) is literally the reverse of the other. Therefore, this pair is a Transpalindromic Square (symbolized by the  glyph). It is the only 4-digit Transpalindromic Square that there is.
glyph). It is the only 4-digit Transpalindromic Square that there is.
In general, you might have already noticed that 9 is a Square (specifically 32) and that 11 is a Palindromic Prime (symbolized by the 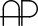 glyph). Let's look more closely at how 9 and 11 affect Squares and Primes...
glyph). Let's look more closely at how 9 and 11 affect Squares and Primes...
Squares and Primes
• 11 is known as the Palindromizer. This is because 11 and its multiples control whether or not a number is Palindromic (i.e.: the same number forward and backward).
• 9 is known as the Transpalindromizer. This is because 9 and its multiples control whether or not a number is Transpalindromic (i.e.: a number which keeps the same quality when reversed, even though the quantity itself changes).
We cannot emphasize this enough: In order to get a full comprehension of number, we need to consider how both of these are continuously appearing throughout all of the other numbers within the base-ten system.
The following diagram is called The Prime/Square Interface. It is one of the ways in which Syndex explains the importance of 9 and 11 within the Squares:
It may seem like a lot is going on within this diagram, but we will take it one step at a time. Here are some of the key features of it:
• The numbers within the right-hand column are Squares derived from the numbers within the left-hand column. In other words, multiply the number on the left by itself to get the number on the right.
• The small arcs on either side of the 1-digit numbers within the left-hand column are showing which ones add up to 9 and 11, while the black dots on either side of the entire left-hand column are marking multiples of 9 and 11. Notice that multiples of 9 and 11 coincide or "sync up" at 99. The Nave of the entire chart is 49.5, like with the multiples of 9 and 11 shown before.
• The arcs made with dashed lines are highlighting significant symmetries within the numbers of both columns. Notice that the center of these arcs align with a muliple of 11, or in-between two numbers that connect to a multiple of 11 in some way (e.g.: 16.5 × 2 = 33). We are mainly focused upon the stretch of numbers between 11, the first 2-digit Palindromic Prime (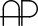 ), and 101, the first 3-digit Palindromic Prime (
), and 101, the first 3-digit Palindromic Prime (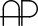 ). This is because 99, 100, and 101 share the same relationship that 9, 10, and 11 do. To put it another way, by looking at the how The 9-11 Cycloflex appears within every group of ten (i.e.: between 10 and 100, between 100 and 1000, etc.), we uncover all of the Archetypal Number Classes and emphasize how important these classifications are! To explore it more in-depth...
). This is because 99, 100, and 101 share the same relationship that 9, 10, and 11 do. To put it another way, by looking at the how The 9-11 Cycloflex appears within every group of ten (i.e.: between 10 and 100, between 100 and 1000, etc.), we uncover all of the Archetypal Number Classes and emphasize how important these classifications are! To explore it more in-depth...
• Both 11 and 101 are Palindromic Primes (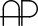 ) that produce the Palindromic Squares (
) that produce the Palindromic Squares (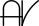 ) of 121 and 10201. Notice 112 = 121 and 1012 = 10201.
) of 121 and 10201. Notice 112 = 121 and 1012 = 10201.
• Transpalindromic Squares (i.e.: Squares which stay Squares when reversed) are contained inside of boxes within the diagram and are marked with the appropriate glyph ( ). There are only two pairs of 3-digit Transpalindromic Squares. They are:
). There are only two pairs of 3-digit Transpalindromic Squares. They are:
144  441
441
and
169  961
961
The numbers in the first pair are made by the Transpalindromic Composites (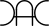 ) 12 and 21. Notice 122 = 144 and 212 = 441. Both 12 and 21 are Composites.
) 12 and 21. Notice 122 = 144 and 212 = 441. Both 12 and 21 are Composites.
The numbers in the second pair are made by the Transpalindromic Primes ( ) 13 and 31. Notice 132 = 169 and 312 = 961. Both 13 and 31 are Primes.
) 13 and 31. Notice 132 = 169 and 312 = 961. Both 13 and 31 are Primes.
These pairings lead to some amazing interactions between The 9-11 Cycloflex and the Squares. Some of them can be demonstrated through diagrams called Syndex Pretzels:
Other "pretzel-like" patterns can be uncovered with a little attention to how 9 and 11 affect other numbers:
• The only 2-digit Retroprime Square (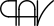 ) is 16, which is 42. Its mirror is 61, a Retrosquare Prime (
) is 16, which is 42. Its mirror is 61, a Retrosquare Prime (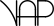 ). This pair of classifications is quite rare.
). This pair of classifications is quite rare.
16 is preceded by 15, a Transpalindromic Composite (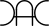 ). 15 is 3 × 5 and 51 is 3 × 17.
). 15 is 3 × 5 and 51 is 3 × 17.
16 is succeeded by 17, a Transpalindromic Prime ( ).
).
Finally, 16 + 61 = 77, which is 7 × 11. There is that 9-11 Cycloflex again!
Now, let's get a better look at Primes specifically...The following diagram is called The Latching Order:
Again, it probably seems more complicated than it actually is. It is okay if the numbers are too small to read. We just want to show the general pattern that they make and we will repeat the numbers that we are referring to below. Here are a couple of the key features of this diagram:
• The numbers within the right-hand column are the Primes, while the numbers in the left-hand column are their place within the sequence. For example, if we were looking for the 149th Prime, then all we need to do is look for 149 in the left-hand column, and then find the number directly across from it within the right-hand column, which is 859. Therefore, the 149th Prime is 859.
• All Palindromic Primes (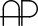 ) are marked by lines with black dots on their ends. There are sixteen of them listed here:
) are marked by lines with black dots on their ends. There are sixteen of them listed here:
11 [the 5th Prime]
101 [the 26th Prime]
131 [the 32nd Prime]
151 [the 36th Prime]
181 [the 42nd Prime]
191 [the 43rd Prime]
313 [the 65th Prime]
353 [the 71st Prime]
373 [the 74th Prime]
383 [the 76th Prime]
727 [the 129th Prime]
757 [the 134th Prime]
787 [the 138th Prime]
797 [the 139th Prime]
919 [the 157th Prime]
929 [the 158th Prime]
• The arcs made with dashed lines are showing Reflective Sets, which are Transpalindromic pairs organized into groups by how many digits they contain. Here are all of the 2 and 3-digit Reflective Sets of Transpalindromic Primes ( ):
):
Reflective Set of 2-digit Transpalindromic Primes ( )
)
13  31
31
17  71
71
37  73
73
79  97
97
There are four in total.
Reflective Set of 3-digit Transpalindromic Primes ( )
)
107  701
701
113  311
311
149  941
941
157  751
751
167  761
761
179  971
971
199  991
991
337  733
733
347  743
743
359  953
953
389  983
983
709  907
907
739  937
937
769  967
967
There are fourteen in total.
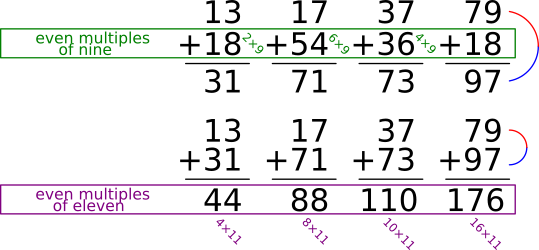
For now, we are only going to look at the 2-digit Reflective Set:
All of them are separated by 9 and 11! Let's look more closely at how they create a symmetry within the stretch of numbers between 1 and 99:
Photo Credit: From the book The Meaning of the Monas Hieroglyphica with regards to Number by Jim Egan
The arcs connect each of the numbers within the 2-digit Reflective Set. If we find their "average" (i.e.: by adding the numbers together and dividing them by how many of them that there are), we get a multiple of 11 that lies directly between them:
13 + 31 = 44 and 44 ÷ 2 = 22
17 + 71 = 88 and 88 ÷ 2 = 44
37 + 73 = 110 and 110 ÷ 2 = 55
79 + 97 = 176 and 176 ÷ 2 = 88
Notice that the arrows point to 22, 44, 55, and 88.
You might be wondering where the other Transpalindromic pair came from (the one highlighted in bold within the above diagram)...
39  93
93
While neither of these numbers is actually Prime, they are very nearly so as 39 = 3 × 13 and 93 = 3 × 31.
The 9-11 Cycloflex definitely makes clear an order to the Primes, Squares, and Composites that is often hidden from view!
Two New Mathematical Operations
We have been continuously using the operation of Retrocity ( ) in our exploration of number thus far. However, you have probably already noticed that we have also been adding together the mirrored numbers in many of the examples above. If we take any multi-digit numeral and repeatedly add it to its mirror, we will eventually reach a Palindromic number. To give a couple of examples...
) in our exploration of number thus far. However, you have probably already noticed that we have also been adding together the mirrored numbers in many of the examples above. If we take any multi-digit numeral and repeatedly add it to its mirror, we will eventually reach a Palindromic number. To give a couple of examples...
Becomes Palindromic in 1 step:
143 + 341 = 484
Becomes Palindromic in 3 steps:
587 + 785 = 1372
1372 + 2731 = 4103
4103 + 3014 = 7117
If there is a trail of one or more zeros at the end of a number, we can just ignore them when we flip it. For example:
330 + 033 = 363
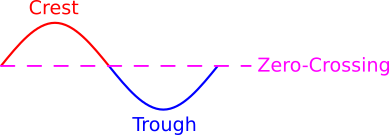
This operation is called finding a Retroadditive Sum. [It is somewhat similar to "Kaprekar's Routine" in traditional mathematics.] Its purpose is to find Palindromes as a point of reference. Remember, Palindromic numbers are always acting like mirrors for other numbers in some way. This is why Naves are often Palindromes. To use an analogy: If the two mirrorings are akin to the crest and trough of a wave, then a Palindrome would be akin to the "zero-crossing", where the wave seems to turn around.
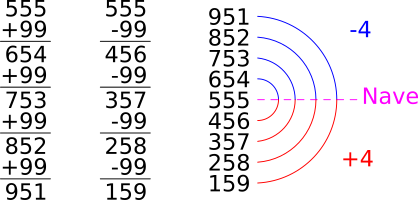
Once we have a Palindromic number, whether by finding the Retroadditive Sum or when encountering one that is naturally Palindromic, then we can add and subtract the multiples of 9 and 11 appropriate to the number of digits that it has in order to uncover more mirrorings. For example:
In this example, we are adding and subtracting 99 from 555. We use 99 because 555, our Palindrome, is a 3-digit number. If it was a 4-digit number, then we would use 1089 (which is 99 × 11). If it was a 5-digit number, then we would use 10890 (which is 990 × 11), and so on.
This operation will be referred to as Cycloscillation. Its purpose is to make plain the octaves inherent to The 9-11 Cycloflex within any set of numbers that we are focused on. Whenever we apply it, we will never get more than four pairs of Transpalindromes. In other words, the pattern of 4 forward and 4 reverse always holds.
In Summary
There is a wave pattern that permeates all of number (The 9-11 Cycloflex), and we can reveal the octaves that it forms through three distinct, yet interrelated, mathematical operations:
• Retrocity ( ) - mirroring the digits within a multi-digit number
) - mirroring the digits within a multi-digit number
• Retroadditive Sum - adding a number to its mirror until we get a Palindrome
• Cycloscillation - adding and subtracting multiples of 9 and 11 from a Palindrome
This sorts the Primes, Squares, and Composites into the twelve Archetypal Number Classes.
While all of this may seem trivial, it is actually very important. It shows a coherence to numbers that is not normally acknowledged, one that can help reveal meaningful connections within any situation in which mathematics is applied. As we continue, we will try to demonstrate some of these connections...
Next Section →
 glyph) is controlled by the numbers 9 and 11. Notice that 9 is one less than our base, and 11 is one more than our base (i.e.: 10 - 1 = 9 and 10 + 1 = 11).
glyph) is controlled by the numbers 9 and 11. Notice that 9 is one less than our base, and 11 is one more than our base (i.e.: 10 - 1 = 9 and 10 + 1 = 11).




 glyph). It is the only 4-digit Transpalindromic Square that there is.
glyph). It is the only 4-digit Transpalindromic Square that there is.
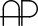 glyph). Let's look more closely at how 9 and 11 affect Squares and Primes...
glyph). Let's look more closely at how 9 and 11 affect Squares and Primes...

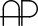 ), and 101, the first 3-digit Palindromic Prime (
), and 101, the first 3-digit Palindromic Prime (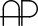 ). This is because 99, 100, and 101 share the same relationship that 9, 10, and 11 do. To put it another way, by looking at the how The 9-11 Cycloflex appears within every group of ten (i.e.: between 10 and 100, between 100 and 1000, etc.), we uncover all of the Archetypal Number Classes and emphasize how important these classifications are! To explore it more in-depth...
). This is because 99, 100, and 101 share the same relationship that 9, 10, and 11 do. To put it another way, by looking at the how The 9-11 Cycloflex appears within every group of ten (i.e.: between 10 and 100, between 100 and 1000, etc.), we uncover all of the Archetypal Number Classes and emphasize how important these classifications are! To explore it more in-depth...
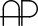 ) that produce the Palindromic Squares (
) that produce the Palindromic Squares (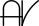 ) of 121 and 10201. Notice 112 = 121 and 1012 = 10201.
) of 121 and 10201. Notice 112 = 121 and 1012 = 10201.
 ). There are only two pairs of 3-digit Transpalindromic Squares. They are:
). There are only two pairs of 3-digit Transpalindromic Squares. They are:
 441
441
 961
961
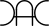 ) 12 and 21. Notice 122 = 144 and 212 = 441. Both 12 and 21 are Composites.
) 12 and 21. Notice 122 = 144 and 212 = 441. Both 12 and 21 are Composites.
 ) 13 and 31. Notice 132 = 169 and 312 = 961. Both 13 and 31 are Primes.
) 13 and 31. Notice 132 = 169 and 312 = 961. Both 13 and 31 are Primes.
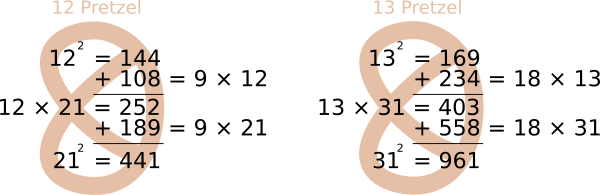

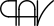 ) is 16, which is 42. Its mirror is 61, a Retrosquare Prime (
) is 16, which is 42. Its mirror is 61, a Retrosquare Prime ( ). This pair of classifications is quite rare.
). This pair of classifications is quite rare.
 ). 15 is 3 × 5 and 51 is 3 × 17.
). 15 is 3 × 5 and 51 is 3 × 17.
 ).
).

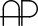 ) are marked by lines with black dots on their ends. There are sixteen of them listed here:
) are marked by lines with black dots on their ends. There are sixteen of them listed here:
 ):
):
 )
)
 31
31
 71
71
 73
73
 97
97
 )
)
 701
701
 311
311
 941
941
 751
751
 761
761
 971
971
 991
991
 733
733
 743
743
 953
953
 983
983
 907
907
 937
937
 967
967
 93
93
 ) in our exploration of number thus far. However, you have probably already noticed that we have also been adding together the mirrored numbers in many of the examples above. If we take any multi-digit numeral and repeatedly add it to its mirror, we will eventually reach a Palindromic number. To give a couple of examples...
) in our exploration of number thus far. However, you have probably already noticed that we have also been adding together the mirrored numbers in many of the examples above. If we take any multi-digit numeral and repeatedly add it to its mirror, we will eventually reach a Palindromic number. To give a couple of examples...
 ) - mirroring the digits within a multi-digit number
) - mirroring the digits within a multi-digit number