Back • Return Home
An Introduction To Mandalogs
It is important to read the previous three articles (The Fundamentals of Syndex, The Classification of Number, and An Introduction To The 9-11 Cycloflex Exemplary Basewave) in order to fully grasp the following. While it may look complex, please have patience for it. It is actually much more simple than it might seem at first. If none of the text makes sense during the first pass, try focusing in on the images before going back and re-reading it.
Contents
• Archetypal Patterns
• The Holotomic Sequence
• Holotomes
• Holotome A [12]
• Holotome B [24]
• Holotome C [72]
• Holotome D [360]
• The Number Seven & The Enneagram
• Holotome E [2520]
Archetypal Patterns
As we saw with The 9-11 Cycloflex, the two-way, wave-like motions throughout the continuum of number generate cycles. Robert Marshall uses the wonderful analogy of a car engine. The pistons within the engine move up and down, which turns a crankshaft to drive the wheels:

We can summarize this archetype with a simple rhyme: An in-and-out pulsation leads to a spiral rotation.
This pattern shows up all throughout Nature, and even within our symbols for describing it! However, the cyclical behavior only truly becomes apparent within numbers when they are placed along the outside of a circle in particular increments. This principle is referred to as Circular Unity, while the 'wheels' of numbers made by this process are called Mandalogs:
Mandalog ["Logical Mandala"] - A number wheel that is Synchrographic in nature. Like a mandala, we can meditate upon its meaning. It acts as a means to transmit large amounts of data experientially. Sometimes, what takes a lot of words to effectively describe can be understood at a glance when a clear image is presented.
The Holotomic Sequence
A Holotome is a particular type of Mandalog. The prefix "holo~" means "whole", while a "tome" is a book, a container for information. Therefore, a Holotome is literally like a "Holographic Book", a gestalt of information about the number continuum as a whole. It is a finite set that contains all of the patterns within it. They are generated through what is called The Holotomic Sequence. This is how it is formed:
6 is the first Perfect Number. Let's take this number, double it, and then multiply the result by each of the Prime numbers in succession, beginning with the number 2:
6 doubled is 12
12 × 2 = 24,
24 × 3 = 72,
72 × 5 = 360,
360 × 7 = 2520,
etc.
Primes are shown in red and Highly Composite Numbers in blue within the above sequence. While this process may seem somewhat arbitrary at first, notice that we are actually generating some of the most "factor-able" numbers (i.e.: Highly Composite Numbers) by means of the least "factor-able" numbers (i.e.: Primes).
Whenever we multiply a number by another, those two numbers become factors of the "product" or result. For example, 2520 is divisible by both 360 and 7 because it is the result of 360 × 7. This operation is referred to as Multiplexing.
If we wanted to produce a number that was divisible by as many consecutive numbers as possible, then we could multiply together every number that came before it. In traditional mathematics, this operation is referred to as a "factorial" and is represented by an exclamation point. For example, say that we wanted a number that was divisible by all of the numbers 1 through 4:
4! = 1 × 2 × 3 × 4 = 24 (which is divisible by 1, 2, 3, 4, and a few multiples of those numbers, like 6, 8, and 12)
This is a simple example. However, this operation quickly produces very large numbers when we use a higher "factorial". If we wanted a number with more consecutive factors, this process can become a bit unwieldy. But notice that every successive number produced within The Holotomic Sequence is divisible by one more of the base numbers than the previous:
12 (the first number to have five of the base-ten numerals as factors: 1, 2, 3, 4, and 6),
24 (the first number to have six of the base-ten numerals as factors: 1, 2, 3, 4, 6, and 8),
72 (a number which has seven of the base-ten numerals as factors: 1, 2, 3, 4, 6, 8, and 9),
360 (the first number to have eight of the base-ten numerals as factors: 1, 2, 3, 4, 5, 6, 8, and 9),
2520 (the first number to have all nine of the base-ten numerals as factors: 1, 2, 3, 4, 5, 6, 7, 8, and 9).
Instead of using factorials, we have produced some of the lowest numbers with as many consecutive factors as possible using the fewest number of multiplications as possible. This phenomenon is called Minimax Factorization within Syndex.
Holotomes
The numbers within The Holotomic Sequence (12, 24, 72, 360, 2520, etc.) are a list of all possible Holotomes. This means we will first make a circle with 12 numbers around its circumference, then a circle with 24 numbers, then one with 72 numbers, and so on.
We will give a letter name to each of these Holotomes in order to distinguish them from one another:
Holotome A = 12,
Holotome B = 24,
Holotome C = 72,
Holotome D = 360,
Holotome E = 2520,
etc.
What is special about these circles of numbers? They make a relationship between the Primes, Squares, and Composites clearly visible. This is because numbers at one part of the continuum can affect others that are seemingly distant from them. For example, 9 is not Prime because 3 comes before it. This is true for every odd number that is a multiple of some Prime. One of the characteristics of all Holotomes is that Primes and multiples of Primes are always in mirrored positions from one another within them. Normally, the distribution of Primes is considered erratic, but here is one way of seeing their hidden symmetry. This two-part quality, which connects numbers to geometry, makes these figures into what Syndex calls Dual Modules.
[There are some concepts out there that produce similar results, such as "Number Spirals" (e.g.: the "Ulam Spiral", Gary Croft's "Prime Spiral Sieve", Scott Nelson's "Daisy Integer Matrix", etc.) and various other "Wheel Factorization"-type algorithms. However, few exhibit symmetry both vertically and horizontally like each of the Holotomes do.]
Let's look at the first Holotome...
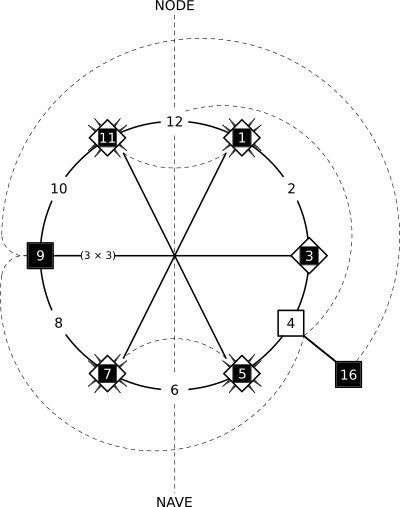
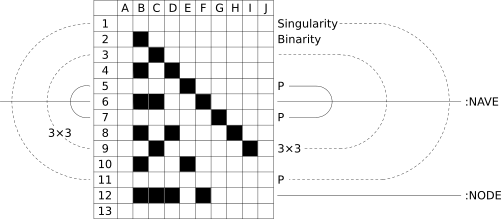
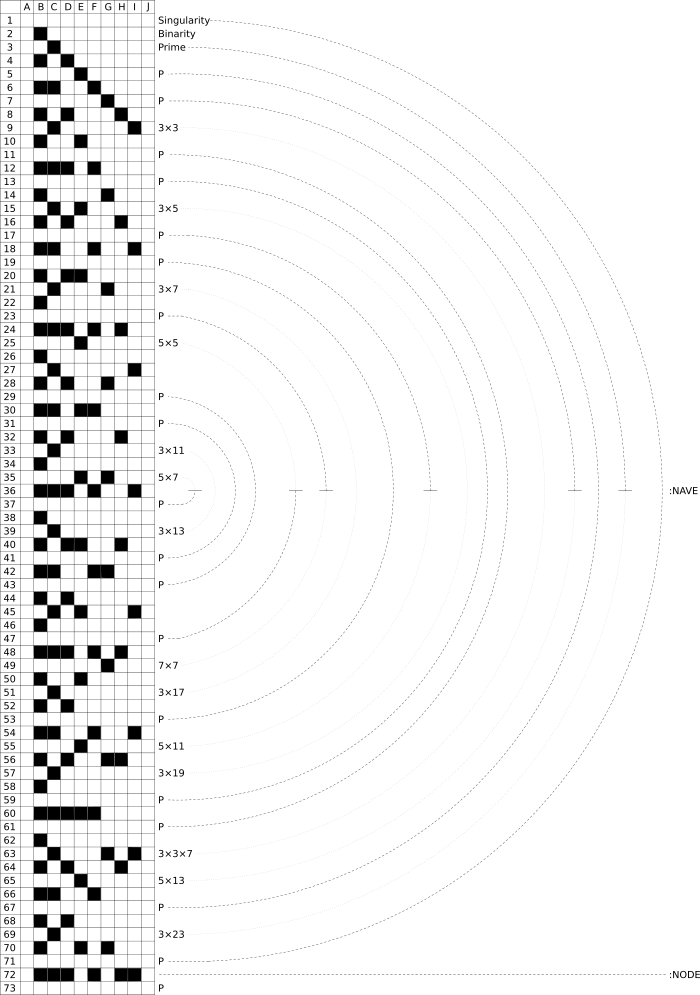
Holotome A [12]
The Node is the total amount of numbers that form the Holotome, while the Nave is the halfway point. The Primes are symmetric around the Nave, almost as if it acts as a mirror. The dotted-line spiral delineates Squares.
The grid is the same information as the circle, but in tabular form. [It is similar to Jeffrey Ventrella's "Divisor Plot".] The little rows of eight boxes (labeled as columns B through I) are one of the ways in which factors are shown in Syndex. It is called a Synchronicity Code. If the second box from the left is darkened (column B), then that number has 2 as a factor. If the third box from the left is darkened (column C), then that number has 3 as a factor, and so on. The reason why column A is usually ignored is because every number is divisible by 1.
Note that columns B through I correspond to our "octave" of numbers 2 through 9. Therefore, sweeping across an entire row immediately shows all of the factors of each number to the left of it, and sweeping down a column shows the multiples of the number associated with that column as a whole. For example, column B is like counting by twos, column C is like counting by threes, and so on.
To put it simply: Columns show multiples, while rows show factors. Because multiplication and division are "inverse operations", multiples and factors are related to one another. Primes, Composites, and Squares (and all of their factors and multiples) are tightly integrated into one cohesive system.
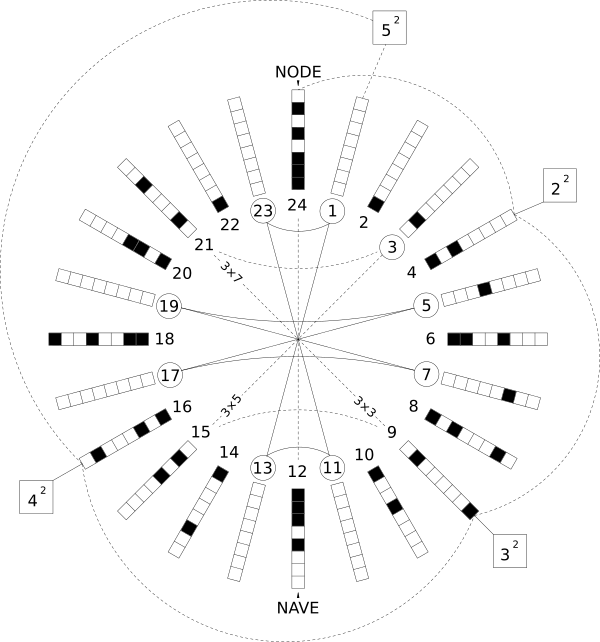
Holotome B [24]
[This is equivalent to Peter Plitchta's "Prime Number Cross".]
The Node of Holotome A has become the Nave of Holotome B. Primes and multiples of Primes are still mirroring across the Nave.
Notice that boxes B through I of our Synchronicity Code are not just in tabular form now, but also exist along the wheel. They are read from the center-out. Each column is now referred to as a Track. Following the Tracks around the entire circle shows the factors and multiples of all of the different numbers, just like the table. When more than one box is darkened within the same row, then those Tracks are said to be "synchronized". This is why it is called a Synchronicity Code.
Holotome C [72]
Node = 72; Nave = 36
Synchronicity Code = Columns B through I (from 2 to 9)
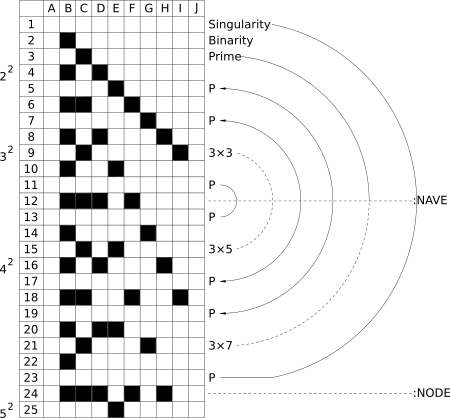
Holotome D [360]
Node = 360; Nave = 180
Synchronicity Code = Columns B through J (from 2 to 10)
The only base-ten factor that is missing from 360 is the number 7...
The Number Seven & The Enneagram
There is much mysticism revolving around the number 7. It embodies many cycles and symmetries throughout the number continuum as a whole. For example, division by seven always yields a repeating decimal that has the same digits in a different order. Notice that 3, 6, and 9 are the only base-ten numbers that are missing from this sequence:
1 ÷ 7 = 0.142857...
2 ÷ 7 = 0.285714...
3 ÷ 7 = 0.428571...
4 ÷ 7 = 0.571428...
5 ÷ 7 = 0.714285...
6 ÷ 7 = 0.857142...
7 ÷ 7 = 1
8 ÷ 7 = 1.142857...
9 ÷ 7 = 1.285714...
etc.
Why does this work? As a whole number, 142857 is referred to as a "Cyclic Number". This means that multiples of it produce another number which are the same digits just shifted over:
142857 × 1 = 142857
142857 × 2 = 285714
142857 × 3 = 428571
142857 × 4 = 571428
142857 × 5 = 714285
142857 × 6 = 857142
142857 × 7 = 999999
Therefore, this sequence shifted over three digits and added to itself produces 9 repeatedly:
142857 + 857142 = 999999
285714 + 714285 = 999999
428571 + 571428 = 999999
Within various spiritual teachings (such as the "Fourth Way"), these patterns are sometimes referred to as "The Law of Seven" and "The Law of Three". They are usually represented by a symbol called The Enneagram (from the prefix "ennea-", meaning "nine"):
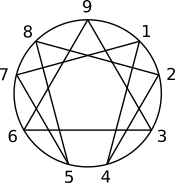
The six-pointed figure within The Enneagram is called a "hexad" (from the prefix "hex-", meaning "six"). It traces out the numbers in the sequence (1-4-2-8-5-7), whereas the triangle traces out the numbers that seem to be missing from it (3, 6, and 9). [These circuit-like patterns are called "Cyclic Permutations" within traditional mathematics.]
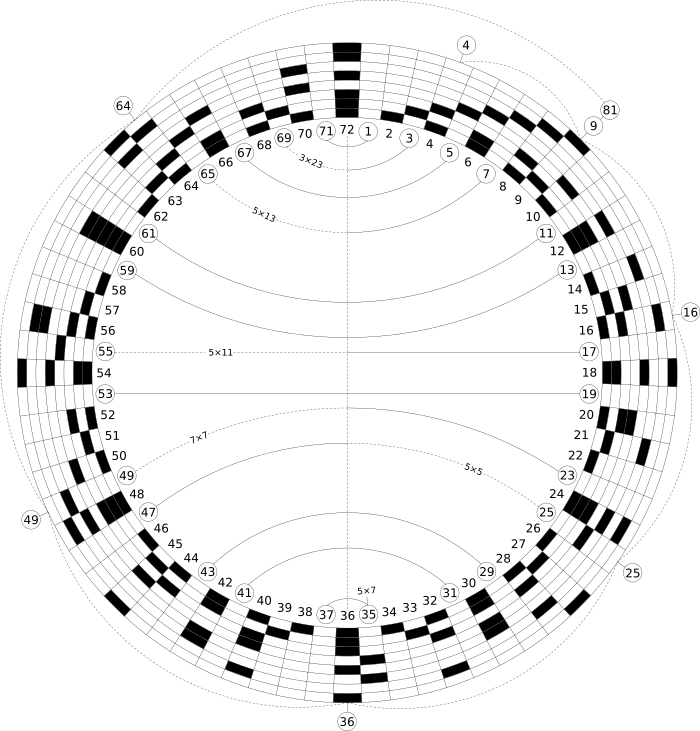
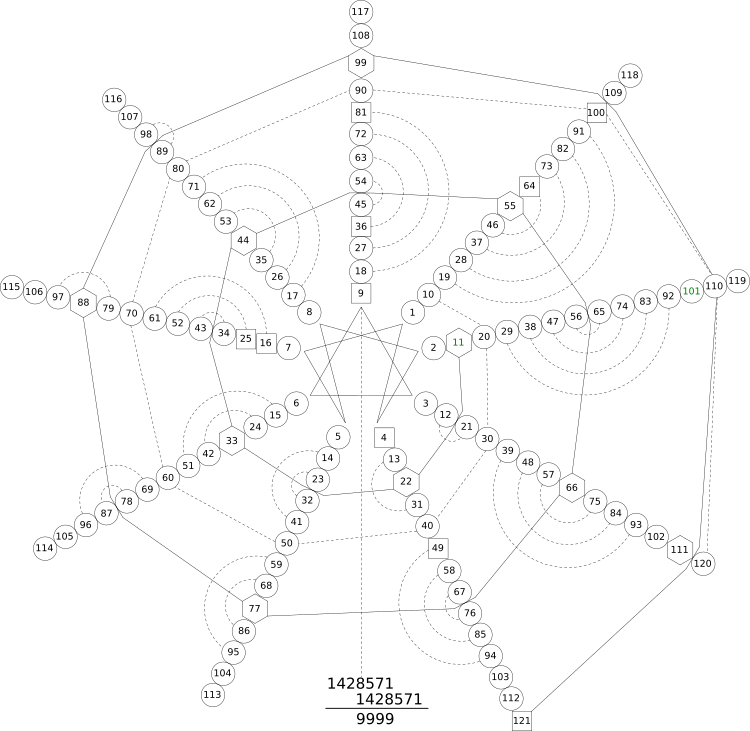
We will use The Enneagram to make another Mandalog:
This number wheel contains 9 "spokes" or "rays", and the entire spiral of numbers is taken out to 121 (which is 11 × 11). Squares are contained within squares. The Palindromic Primes (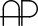 ) 11 and 101 are highlighted in green. Other than 11, all Palindromic Composites (
) 11 and 101 are highlighted in green. Other than 11, all Palindromic Composites (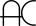 ) are contained within hexagons. The dotted-line spiral shows multiples of 10, while the solid-line spiral shows multiples of 11. Following the solid-line spiral shows how the Palindromic Composites make mirrors in which adjacent numbers are reflected. Notice that the number of mirrorings never exceeds 4 pairs of numbers within each "spoke", and that the pattern of the mirrorings themselves mirrors across the entire solid-line spiral.
) are contained within hexagons. The dotted-line spiral shows multiples of 10, while the solid-line spiral shows multiples of 11. Following the solid-line spiral shows how the Palindromic Composites make mirrors in which adjacent numbers are reflected. Notice that the number of mirrorings never exceeds 4 pairs of numbers within each "spoke", and that the pattern of the mirrorings themselves mirrors across the entire solid-line spiral.
Now, let's get to Holotome E (which is generated by 360 × 7)...
Holotome E [2520]
[In Progress...]





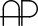 ) 11 and 101 are highlighted in green. Other than 11, all Palindromic Composites (
) 11 and 101 are highlighted in green. Other than 11, all Palindromic Composites (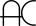 ) are contained within hexagons. The dotted-line spiral shows multiples of 10, while the solid-line spiral shows multiples of 11. Following the solid-line spiral shows how the Palindromic Composites make mirrors in which adjacent numbers are reflected. Notice that the number of mirrorings never exceeds 4 pairs of numbers within each "spoke", and that the pattern of the mirrorings themselves mirrors across the entire solid-line spiral.
) are contained within hexagons. The dotted-line spiral shows multiples of 10, while the solid-line spiral shows multiples of 11. Following the solid-line spiral shows how the Palindromic Composites make mirrors in which adjacent numbers are reflected. Notice that the number of mirrorings never exceeds 4 pairs of numbers within each "spoke", and that the pattern of the mirrorings themselves mirrors across the entire solid-line spiral.