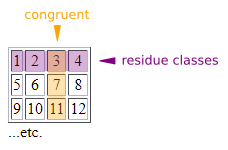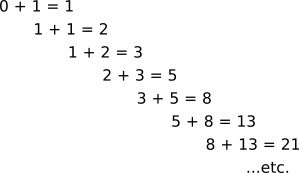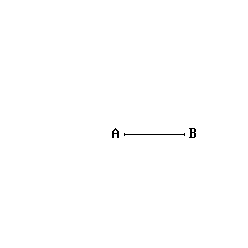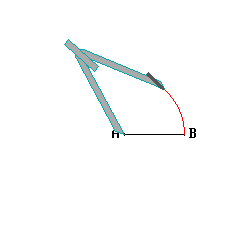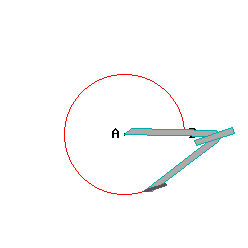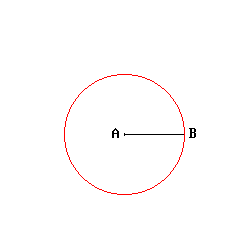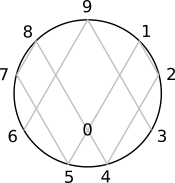Back • Return Home
The Universe: A Play In Four Acts
Here we will endeavor to share some mathematical and musical tools for understanding reality in great detail. While it may sound complicated, we will attempt to make all of it very simple to understand. Only basic Arithmetic (i.e.: the ability to add, subtract, divide, and multiply) and basic Geometry (i.e.: the ability to recognize shapes) will be needed. It may seem like a lot of text, but please have patience for it and try to visualize what is described as you read.
Contents
• Act 1: The Archetype of Vibration
• Act 2: The Archetype of Rotation
• Act 3: The Archetype of Nesting
• Act 4 (Grand Finale): Unity
Act 1: The Archetype of Vibration
Literally everything manifest is vibrating in some manner. We measure these regularly repeating motions by how many of them occur in one second and call it "frequency". More vibrations per second = "high frequency", and less vibrations per second = "low frequency".
Sound is a vibration. Everytime that we hear a single sound, we are actually hearing more than just that sound alone. We also hear multiples of that frequency occurring at the same time. We will represent the sound we start off with as 1, and the multiples as ×2, ×3, and so on. Like this:
1
×2
×3
×4
×5
...etc.
The 1 is referred to as the "fundamental", while the ×2, ×3, etc. are usually called "harmonics" or "overtones". That makes this entire sequence an "overtone series". This overtone series is very important to music and explains much about why we hear things in the ways that we do. For example, two instruments sound different from one another, even if they are playing a sound of the exact same frequency, because the harmonics that they make are of different volumes (e.g.: due to those instruments having a different structure, being made from different materials, etc.). In music, this is called "timbre".
Indeed, the overtone series explains many things about vibration, but we will return to this idea in a moment...
A "ratio" is the relationship between two units. For example, if we have a ratio of "2:1" (read as "two-to-one"), then we can say that for every 2 of something we have 1 of something else. [If we would like to be fancy, in mathematics, the first number is called the "antecedent" and the last number is called the "consequent". In this case, 2 is the "antecedent" and 1 is the "consequent".]
Now, let's turn every two consecutive numbers within the overtone series into a ratio, like this:
1:2
2:3
3:4
4:5
...etc.
These ratios are also very important to music. They are called "intervals", and they determine how we interpret the relationship between two sounds. For example, if we have two sounds whose frequencies are in a ratio of 2:1 (i.e.: one is double or half the frequency of the other), then those sounds seem very much alike, so much so that we interpret them as the same sound. It is just that one of them seems to be moving a little faster or slower than the other. In other words, one is of a higher frequency and the other is of a lower frequency. This is called "pitch" in music.
In much of the music of the "west" (i.e.: across much of North America and Europe), we represent all pitches with the first seven letters of the Roman alphabet, A through G. This is because the same patterns repeat over and over again, no matter how high or low the frequencies involved. If we run out of letters to represent them, then we just repeat the cycle:
A, B, C, D, E, F, G, A, B, C, D, E, F, G, ...and so on.
The intervals also have special names that are determined by how many of these letters two frequences of sound encompass. Some examples:
• From A to B is called a "second" (not to be confused with the measure of time) because it encompasses two letters, in this case, A and B.
• From A to C is called a "third" because it encompasses three letters, in this case, A, B, and C.
• From A to D is called a "fourth" because it encompasses four letters, in this case, A, B, C, and D.
...etc.
Notice that these letter sequences are always in alphabetical order, and when we go from A back to A again in a loop, then we are encompassing eight letters. This is where we get the term "octave" (from the prefix "oct-" meaning "eight"). In short, we have an A representing a lower frequency, and another A representing a higher frequency. Or to put it another way, an "octave" is just an interval of 2:1.
This same kind of "musical language" can be used to describe any kind of vibration, not just what we interpret as "sound". Further, we can make visual representations of different kinds of vibrations, such as with a machine called an "oscilloscope".
Photo Credit: Tektronix
This might look like a complicated device, but the idea behind it is simple: A tool called a "probe" connects to it (the black attachment in the image above). The probe picks up a vibration and the oscilloscope turns that signal into a visual representation called a "wave" (short for "waveform") on its screen.
If the oscilloscope picked up two signals in the ratio of 2:1, then it could generate an image like this:
Photo Credit: ???
These types of waves are called "Lissajou Figures". There are other kinds of Lissajous Figures for vibrations that are in different ratios to one another, but this is the pattern that we will focus on here. The reason why this particular shape is related to the ratio of 2:1 is because we are moving two times in the horizontal direction every time we move once in the vertical direction:
You might have already noticed that this wave is equivalent to a "figure-eight", an "infinity symbol" ∞ [or to use the fancy mathematical term, a "lemniscate"]. This is not by accident. "Infinity" describes something without beginning or end, something that loops back into itself (or is "self-reflexive"). We will see just how appropriate this symbol is...
Act 2: The Archetype of Rotation
Everything manifest is also rotating in some manner, although it may not always be easy to see. From the swirling of vortices in the water and air all around us, to the spin of the planet that supports us, rotation is ubiquitous throughout Nature. It shows up everywhere!
There is already plenty of mathematics for describing rotation (especially as it occurs within various branches of science). We will take a completely different approach to this subject here, one that uses simple numbers. How this approach is related to rotation may not be readily apparent, but it will become more clear as we continue on. First, let's talk about numbers...
Numbers are symbols. Oftentimes, these symbols are used to express quantities. For example, we could have two apples or five pencils, or "two" and "five" of any objects really. However, numbers themselves also follow patterns. As another example, we do not have to invent a new symbol everytime we wish to describe a larger amount. We simply use the same symbols in a different order. In mathematics, this is called "place value" (i.e.: the "place" or order of the symbol determines the "value" or amount it represents).
A "number base" is how many symbols we use to represent all quantities at any given moment. We usually use ten different symbols, 0 through 9:
0, 1, 2, 3, 4, 5, 6, 7, 8, and 9
Because we are using ten symbols, this is referred to as a "base of ten", or just "base-ten" for short. [If we want to be extra-fancy, then we could say that we are using a "radix of ten". "Radix" is another word for number base.]
Let's see if we can uncover more patterns. We will use our base-ten numbers to make a table counting up to 4, and jump back to the beginning of the table for every group of four, like this:
| 1 |
2 |
3 |
4 |
| 5 |
6 |
7 |
8 |
| 9 |
10 |
11 |
12 |
...etc.
In mathematics, the size of the group that we are placing the numbers into is called a "modulus" (or just "mod" for short). In this case, we can say that we have just made "a modulus of 4".
Notice that in every column of the table, the next number is 4 away from the previous one in the same column. For example, in the first column:
1 + 4 = 5,
5 + 4 = 9,
...etc.
We are just adding 4 each time to get the next number in the column.
There is a shorthand way for referring to numbers that fall within the same column, no matter how far down the column we may go. It is called "congruence", and we can write out this relationship like this:
5 ≡ 1 (mod 4)
This would be read as "5 is congruent to 1 in mod 4". This just means that when we separate our numbers into groups of four, 5 and 1 are in the same column. Notice that the symbol for congruence looks like an equals sign, but it uses three lines (≡) instead of two (=). Please do not get them confused! Let's look at one more example just to be clear:
9 ≡ 1 (mod 4)
This would be read as "9 is congruent to 1 in mod 4", and again, this just means that 9 and 1 share the same column when we separate our numbers into groups of four. There is another way to talk about this relationship though...
Division is also to separate items into groups of equal size. Therefore, it is as if we are dividing every number on the table by 4. For example:
5 ÷ 4 = 1R1
9 ÷ 4 = 2R1
...etc.
Numbers in the same column will always have the same remainder (i.e.: that left over part when a number does not divide evenly). This remainder will always be the first number in the column, no matter how high we may go. For example, in the second column:
10 ÷ 4 = 2R2
Notice that 10 has a remainder of 2 when divided by 4, and 10 is in the same column as the one with 2 at the top. Let's look at one more:
7 ÷ 4 = 1R3
7 has a remainder of 3 when divided by 4, and it is in the same column as the one with 3 at the top.
In mathematics, there is a special name for all of the remainders in the first row of our table, no matter how large the table is. They are called "residue classes". That might sound like a weird name, but it makes sense if we think of a remainder as something left over, a "residue" left behind by the other numbers.
However, there is one exception here: Every number in the fourth column divided by 4 is going to have a remainder of 0 because that column only has multiples of 4. For example:
8 ÷ 4 = 2
12 ÷ 4 = 3
...etc.
Notice that there are no remainders with any number in the 4's column when it is divided by 4. This means that 0 and 4 are seen as equivalent in a modulus of 4.
In summary:
• The modulus is how large our grouping is (in this example, we are splitting all numbers up into groups of 4).
• All numbers within the first row are residue classes. They are the remainders when dividing every number in the table by the modulus.
• All numbers within the same column are congruent. In other words, they share the same residue class.
Why bother with all of this? It allows us to represent a very large group of numbers with a much smaller set of numbers. This is called a "residue number system". To put it another way, instead of making the entire table each time, we can represent all of the numbers within it by just the numbers in the first row (i.e.: the residue classes). This will become an incredibly useful tool later on.
But before we continue, there is one more pattern that we will cover here because it is very important. Something interesting happens when the modulus is one less than the base. Notice that 10 - 9 = 1. So, as an example, let's make a modulus of 9 with our base-ten numbers, like this:
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
| 19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
...etc.
We find that by adding up the digits in any multi-digit number continuously until we get a single digit, we end up with the corresponding residue class. In other words, pick any number out of the table and add together its digits until you get a single-digit number:
10 ≡ 1 (mod 9) because 1 + 0 = 1
19 ≡ 1 (mod 9) because 1 + 9 = 10 and 1 + 0 = 1
...etc.
Adding together the digits always makes the first number within the same column! This process has many names depending upon the context, but it is generally referred to as "finding the digital root". The "digital root" is the sum you end up with. Again, it is equivalent to the remainder that is left behind when we divide that number by the size of the modulus. Whew! That sounds like a mouthful....Just remember, add the digits together until you get a single digit to find the underlying pattern.
Everything that we have covered thus far is part of a specific branch of mathematics called "modular arithmetic". It might seem strange, but it is likely that you already use it everyday in some form. For example, there is no "13th hour" on an analog clock. It goes up to 12 before cycling back to 1.
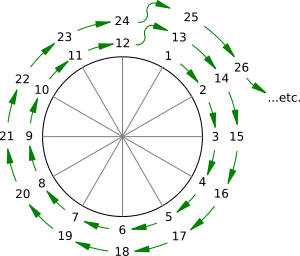
Surprise! We've just found out how rotations can be represented as simple numbers. Instead of representing the modulus as a zig-zagging table, we can view it as a spiral of numbers around the outside of a circle, like this:
The modulus is the number of spokes in the wheel. The more turns of the spiral, the more numbers in the table.
Act 3: The Archetype of Nesting
Everything manifest is nested inside of something. We are a system embedded within ever larger systems. Think of a "Matryoshka" (or Russian nesting doll):
...Or the "Droste Effect", where there is a picture within a picture continuously:
What is an efficient way to describe this mathematically?
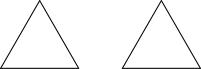
In geometry, if two figures are the same size and same shape, then we say that they are "congruent". For example, here we have two congruent triangles:
Notice that the length of all of their sides are the same.
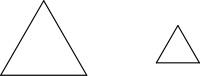
If two figures are the same shape but different sizes, then we say that they are "similar". Here are two similar triangles:
In this case, one triangle is twice the size of the other. We could say that their sizes are in a ratio of 2:1. [Another way to think about this is to realize that, even though the length of their sides are different from one another (i.e.: one is twice as long), the angle between those sides is the same for both triangles. The "angle" is just the amount that those lines are spread apart; it is measured in "degrees". Therefore, we can think of all of the "vertices" (or corners where two lines meet) within both of these triangles as representing 60-degree angles.]
This is why ratios are so important! They let us scale something up and down in size without changing its shape. [The extra-fancy mathematical term for this is "scale invariance", meaning that they stay the same or "invariant" no matter what level of "scale" or size that they are applied to. A triangle is still a triangle no matter how large or small it is.]
Now, let's make a figure and place a copy of itself inside of itself, like this:
Notice that the contents of the red circle are a smaller copy of what is inside of the blue circle.
We would say that this figure is "self-similar". "Self-similarity" is just nesting. Let's see if we can take these sorts of nesting patterns further...
Just as a ratio is two wholes compared, we can compare two ratios to each other to see if they are equivalent. This is called a "proportion". For example, let's take the ratios 2:1 and 4:2. As a proportion, we could write them as:
2:1 = 4:2
This would be read as "two is to one as four is to two". In other words, 2 and 1 have the same relationship to each other as 4 and 2. Each number in the set has its own name as well. In this case, the two 2's would be called "extremes", and the 1 and 4 would be called "means". The extremes are on the outside of the proportion and the means are on the inside of the proportion.
Notice that the ratio 2:1 can become the ratio 4:2 if we were to multiply each of the numbers by 2. Or we can divide each number in the ratio of 4:2 by 2 to get 2:1. Therefore, we know that these two ratios are the same even though they use different numbers. Of course, finding this out is trivial with such small and easy to relate numbers. However, there is another way to see if they are the same.
If we multiply the means together and the extremes together and the answer is the same for them both, then those ratios are equivalent. For example:
2 × 2 = 4
and
1 × 4 = 4
Both of them equal 4. Therefore, the ratios 2:1 and 4:2 are describing the same relationship.
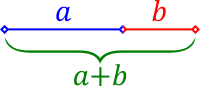
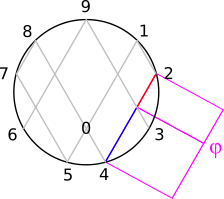
These kinds of proportions are simple, but there is a a special type of proportion called a "Golden Mean" (represented by the Greek letter φ, "phi"). It is a perfect reflection of nesting.
In this diagram, the length of the lines is such that the ratio of the smallest segment (b) to the larger segment (a) is equal to the ratio of the larger segment (a) to the line as a whole (a + b). In other words, it is a proportion, b:a = a:a + b. Notice how it describes a kind of self-similarity.
This Golden Mean Proportion shows up in many shapes that are prevalent throughout Nature on every level of scale, from the microcosm to the macrocosm. We won't go too deeply into it here, but this pattern alone is like a "golden thread" interconnecting everything in the Universe.
Another very common mathematical pattern that is often mentioned in reference to the Golden Mean Proportion are the so-called "Fibonacci Numbers". They are a sequence of numbers generated with this equation:
Fn = Fn-1 + Fn-2
where F0 = 0 and F1 = 1
While this might look complicated, it is actually describing a very simple process. We will start off with two numbers, in this case, 0 and 1. These are called our "seed values". Then, we will add them together to form a third number, like this:
0 + 1 = 1
We can keep looping back our output to become our input over and over again in order to make more numbers:
This process of looping back is called "recursion", while each time we do it is an "iteration". [The equation that describes this kind of procedure is generally known as a "recurrence relation".]
Notice that we eventually end up with this sequence of numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, ...etc.
These "Fibonacci Numbers" also seem to show up all throughout Nature. A good example is from the field of biology known as "Phyllotaxis", which looks at the mathematical patterns inside of plants. The double spirals made by various plant features are often made up of two consecutive Fibonacci Numbers [which are called "parastichy numbers" within the context of Phyllotaxis]:
Photo Credit: Scott Hotton
It turns out that the sequence of Fibonacci Numbers also makes a cycle! If we find the digital root of each number, it will eventually make a repeating pattern of 24 numbers:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9, ...repeat.
[This is called a "Pisano Period" within mathematics.] Notice that we have taken a seemingly endless sequence of numbers that appears throughout Nature and have shown that they actually make a repeating cycle.
Act 4 (Grand Finale): Unity
Let's take everything that we have learned thus far and integrate it into a single diagram. In order to follow along, you will need:
• A calculator
• A flat surface to work on
• A sheet of paper
• A pencil
• A ruler / straight edge (for making lines)
• A drafting compass (for making circles)
First, a quick rundown on how to do compass and straight edge constructions...
Two points (here labeled A and B) can be used to make a line:
Photo Credit: Aldoaldoz
Two points can also be used to make a circle:
Photo Credit: Aldoaldoz
The green dots in the following image show that...
• Two lines can overlap to form another point
• Two circles can overlap to form two points
• A line and circle can overlap to form two points
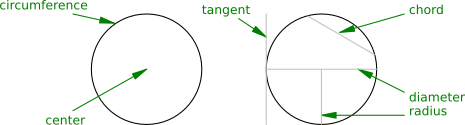
Although you probably already know them, each part of a circle also has a distinct name:
• Circumference - The outer boundary; every point on the circumference of a circle is the same distance from its center
• Radius - A line connecting the center of a circle to its circumference
• Diameter - A line passing through the center of a circle that connects two points on its circumference
• Chord - A line that connects two points on the circumference of a circle without passing through its center
• Tangent - A line passing through only one point on the circumference of a circle
This is all of the basic information that we need in order to understand how to use a compass and straight edge for making shapes. [The fancy mathematical term for this activity is "synthetic geometry" because we are "synthesizing", or putting together, shapes.] Let's get to constructing!
Step 1: Use the drafting compass to draw a circle.
Step 2: Keeping the compass open to the same size, draw another circle on the circumference of the previous one.
Step 3: Everywhere that they overlap, continue to make circles of the same size until there are 6 circles around 1.
Step 4: Using three of the points on the circumference of the central circle, make a triangle.
Step 5: Draw diameters that connect each corner of the triangle to each of the other three points directly across from them.
Step 6: Use the points made by the overlap of the lines in the previous step and the sides of the triangle to make three chords.
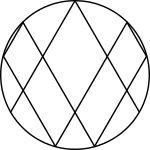
Step 7: Connect together the six points that we just made with four more chords in the following pattern:
Step 8: We will erase all of the extra guidelines and only keep what we need.
Step 9: Finally, we will assign each of our base-ten numerals to various points within the diagram.
While this layout may seem arbitrary, it is far from it. Let's extract part of the pattern and inspect it more carefully:
This looks like the Lissajous Figure for the octave that we saw in Act 1. It embodies it in more than just looks. The numbers also make a ratio of 2:1. Time to grab our calculator! For example, 1 doubled is 2, 2 doubled is 4, and 4 doubled is 8:
But how do move from 8 to 7? We must apply what we learned in Act 2. By finding the digital root of our doublings we close the loop:
8 doubled is 16, and 1 + 6 = 7; 16 ≡ 7 (mod 9)
16 doubled is 32, and 3 + 2 = 5; 32 ≡ 5 (mod 9)
32 doubled is 64, and 6 + 4 = 10; 10 ≡ 1 (mod 9)
...etc.
This pattern of 1-2-4-8-7-5 will continue forever, no matter how high the numbers become. We can reverse our direction through it to halve as well:
1 halved is 0.5, and 0 + 5 = 5
0.5 halved is 0.25, and 2 + 5 = 7
0.25 halved is 0.125, and 1 + 2 + 5 = 8
0.125 halved is 0.0625, and 6 + 2 + 5 = 13; 13 ≡ 4 (mod 9)
...etc.
Notice how a change in operation, from multiplying (doubling) to dividing (halving), is merely a change in direction within the diagram, yet the relationship between the numbers always stays the same! Further, if multiplying and dividing are just faster ways of adding and subtracting, then it is as if we are doing all of the basic arithmetic operations simultaneously!
Now for something very important: The pattern will also hold when we use numbers outside of those that we would naturally get from either doubling or halving from 1. For example, let's take the number 13. We know immediately that 13 ≡ 4 (mod 9) because 1 + 3 = 4. Will it still make the sequence of 1-2-4-8-7-5 if we double or halve it?
| Halving |
Doubling |
| 13 ÷ 2 = 6.5 and 6 + 5 = 11 ≡ 2 (mod 9) |
13 × 2 = 26 and 2 + 6 = 8 |
| 6.5 ÷ 2 = 3.25 and 3 + 2 + 5 = 10 ≡ 1 (mod 9) |
26 × 2 = 52 and 5 + 2 = 7 |
| 3.25 ÷ 2 = 1.625 and 1 + 6 + 2 + 5 = 14 ≡ 5 (mod 9) |
52 × 2 = 104 and 1 + 4 = 5 |
| ...etc. |
...etc. |
Sure enough, 1-2-4-8-7-5 appears both forwards and backwards. We will call this sequence The Doubling-Halving Circuit.
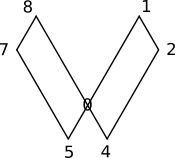
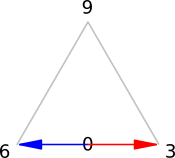
What about the other numbers? Let's focus in on a specific part of the pattern again:
Like The Doubling-Halving Circuit, the 3 and 6 also make a doubling and halving pattern that oscillates back-and-forth across 0 or 9 (as shown by the red and blue arrow in the diagram above):
| Halving |
Doubling |
| 6 ÷ 2 = 3 |
3 × 2 = 6 |
| 3 ÷ 2 = 1.5 and 1 + 5 = 6 |
6 × 2 = 12 and 1 + 2 = 3 |
| 1.5 ÷ 2 = 0.75 and 7 + 5 = 12 ≡ 3 (mod 9) |
12 × 2 = 24 and 2 + 4 = 6 |
| ...etc. |
...etc. |
We will call this pulsation of 3 and 6 across the 0 or 9 as The Gap Space.
Interestingly, wherever The Gap Space crosses The Doubling-Halving Circuit, a Golden Mean Proportion is created!
...So why are we pointing all of this out? More than just a seemingly "random" collection of connections, this diagram is demonstrating some very important information. One of these pieces of information is the fact that the base-ten number system is actually composed of two smaller interpenetrating number systems that interlock and interact in a specific way:
• One of these is based on 2's (i.e.: The Doubling-Halving Circuit)
and
• One of these is based on 3's (i.e.: The Gap Space)
However, The Doubling-Halving Circuit and The Gap Space are just a few of the many intriguing mathematical patterns within this diagram. When one knows how to intepret and apply them, the information one can derive from it quickly penetrates into the depths of every spiritual and scientific teaching currently known to humankind and beyond. That may sound like a bold claim, and to fully demonstrate it takes much patience and prior knowledge. But let's see if we can begin to uncover some of it together:
Science uses mathematics as a language to describe reality. However, number is "pre-mathematical" in that quantity exists before there is a language to describe it. Therefore, at its root, mathematics is not something invented, but something discovered. The patterns that numbers make in relation to one another imply an underlying geometry inherent to number itself. The diagram that we constructed together is that geometry. All numbers of every kind, no matter whatever the context, will always interrelate in this pattern in some manner (although it might not always be apparent as to how). It can also be taken further...
What if we could make a 1-to-1 correspondence between numbers and reality to where their patterns could be used to describe it more directly? We can, and one way of bridging this gap is by realizing that numbers are also equations. For example, in the equation 2 + 2 = 4, the equals sign tells us that everything to the left of it is equivalent to everything to the right of it. It does not matter how complicated the part on the left is, say if it had more numbers or operations. As long as it stays consistent, it will still reduce to a particular number, the one on the right. Therefore, all equations (even all of the most seemingly complicated looking equations used throughout science to describe physical things) are reducible to the same geometry. Again, in order to demonstrate this would require quite a bit more involvement and I am willing to explore it in-depth with whomever is sincerely interested, but we can lightly touch upon it here by way of analogy, symbolism, and correspondence. Please have patience for it as what is being conveyed is quite subtle...
You might have already noticed that the diagram is essentially a modulus of 9, being a circle with 9 numbers around its circumference:
Therefore, all numbers are separated by 9 within it. For example:
1 + 9 = 10 and 1 + 0 = 1
10 + 9 = 19 and 1 + 9 = 10 ≡ 1 (mod 9)
19 + 9 = 28 and 2 + 8 = 10 ≡ 1 (mod 9)
...etc.
Notice that whenever we add or subtract 9 (or a multiple of 9) from any number, it will always give the same digital root. In this case, 10, 19, 28, etc. all reduce to 1. They are all 9 away from one another, so the addition or subtraction of 9 did not alter their digital root. In other words, we can use any number that has a digital root of 9 to scale everything else up or down without changing it. This is because 9 and 0 are equivalent whenever we use a modulus of 9.
Nine holds a special place within this system because it symbolizes something that is unchanging, perfectly balanced and omnipresent throughout, like a fundamental level of reality that interconnects everything, a "unified field" if you will.
To continue, you have probably already noticed that both halves of the diagram are made up of even and odd pairs of numbers that add up to 9. We will call these Polar Number Pairs:
0 + 9 = 9
1 + 8 = 9
2 + 7 = 9
3 + 6 = 9
4 + 5 = 9
Also notice that the 3 and 6 of The Gap Space are the only numbers directly connected to 9. This is because the numbers 3 and 6 are like a "Cosmic Father" and "Mother", a complementary pair of forces that arises from that "unified field" to generate All of existence.
This might sound very abstract, but we can show a representation of this within the diagram by demonstrating the relationship between The Gap Space and The Doubling-Halving Circuit...
If we take all of the lines that are shifted towards the 3, they will add up to 3, and all of those shifted towards the 6 will add up to 6:
 |
 |
| 8 + 7 = 15 ≡ 6 (mod 9) |
1 + 2 = 3 |
| 9 + 6 = 15 ≡ 6 (mod 9) |
9 + 3 = 12 ≡ 3 (mod 9) |
| 1 + 5 = 6 |
8 + 4 = 12 ≡ 3 (mod 9) |
| 2 + 4 = 6 |
7 + 5 = 12 ≡ 3 (mod 9) |
In short, the in-and-out pulsation of the 3 and 6 are actually generating the clockwise (CW) and counter-clockwise (CCW) rotation of the 1-2-4-8-7-5, while the 9 centers All of it. To explain it another way, we might use an analogy that we will call "The Loom of Creation":
The 3 and 6 would be like the longitudinally moving "warp" threads in this loom, while the 1-2-4-8-7-5 would be like the transversely moving "weft" threads that wrap around them...
Photo Credit: Wikipedia
...together they make up the fabric of Space and Time! Everything is a thread within this grand tapestry, and it is woven by something that both transcends and is immanent throughout the entire process. That "something" sounds a lot like what some might call "God" doesn't it?
In fact, this diagram is called The Fingerprint of God. How can God have a "fingerprint"?
Your fingerprints are your identifier. These whorls are wholly unique to you, and on anything you that touch, you leave them behind. Likewise, the Creator leaves "fingerprints" (or archetypal patterns) on everything created.
Photo Credit: Family Court Injustice
The next article will develop this mathematics further and start to connect it to science.
Thank you for reading! ♥