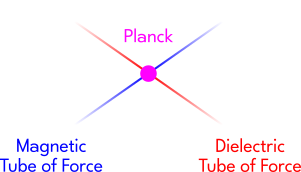
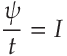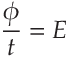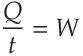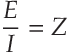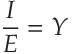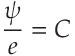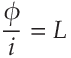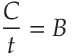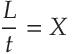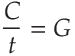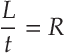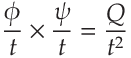A collection of both of these types of tubes is usually called an "electromagnetic field", or simply "electricity". Eric calls the crossing point of both tubes a "Planck", after the work of Max Planck. Max did some math that lead to the concept of a "photon". The "photon" is sometimes used in a manner analogous to Eric's Planck, but we will stick with his description instead. As he states, the Planck is simply "a quantum unit of electro-magnetic induction". A "quantum" is a discrete step, and Plancks can only change in quantities which are discrete steps (i.e.: they can only be represented by whole numbers, nothing fractional). The equation from which we derived the Planck is also similar to what is now known as a "Poynting vector", after the work of a scientist named John Henry Poynting.
Eric generally eschews many of the modern physics interpretations of these older experiements and the theories that arose from them. This is because they have a tendency to obscure important information, especially within the practice of electrical engineering. For example...
According to J.J. Thomson, the scientist who orginally discovered the "electron", an atom literally has thousands of "electrons" and each "electron" is the end of a single tube of Dielectricity. This is
very different from the models of the atom that were formulated afterwards (such as the "Rutherford-Bohr Model"), which show atoms that contain a much smaller number of "electrons" (on the order of tens rather than thousands).
Likewise, the "Electron Theory" states that the electromagnetic field is generated by the movement of "electron" particles within the atoms of a "conductor", such as a copper wire. These "electron" particles have mass. However, Eric is pointing out that these fields are generated as the result of something happening to an Aether and the phenomenon of electricity is "mass-free". In other words, while having a distinct existence that we can interact with, electricity is not "material" in the usual sense of the word.
Not only does the "Electron Theory" affect the equations that are used to describe the situation (by introducing concepts like mass), it also leads to interpretations of how various electrical components function that can be misleading. For example, "capacitors" are devices which store Dielectricity. They are essentially a piece of glass (an "insulator") sandwiched between two metal plates. In "Electron Theory", capacitors are treated as if "electrons" accumulate on the surface of these plates. But we can use a "
dissectible capacitor" to show that Dielectricity is actually held within the glass itself! In other words, it goes towards Counterspace. The "insulator" is really an "absorber".
Similarly, Magnetism is completely expelled from a "conductor" during the phenomenon of "superconductivity". This is called "Meissner Effect". This means that "conductors" could be more properly thought of as "reflectors".
Notice that we regularly use the terms "conductor" and "insulator" in ways that are opposite from what they are actually doing! There are quite a few things that seem backwards within modern physics.
This latter one is related to what most people would call "Current" now (or more properly, "Conduction Current"). If EMF describes the build up of the Magnetic tubes of force around a metallic structure, then MMF would describe the flow of Magnetic tubes of force through it.
This situation is inverted from the previous. If Displacement Current describes flow of the Dielectric tubes of force through a dielectric, then Electrostatic Potential would describe the build up of Dielectric tubes of force around it.
These types of relationships are usually introduced in a simplified way that is referred to as "The Ohm's Law Triangle". It looks something like this:
In this context, "Current" means MMF (what we symbolized by a lowercase
i above) and "Voltage" means EMF (what we symbolized by an uppercase
E above). "Resistance" has the same meaning (what we symbolized by
R above).
The reason why they are arranged in this manner is because it makes it easy to remember how they interrelate mathematically:
And from this, we can derive the following equations:
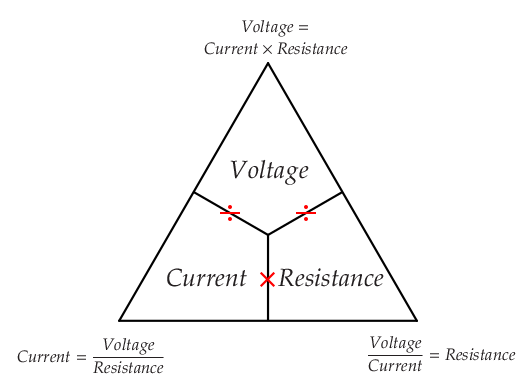
Similar things are sometimes done within physics for the equations related to Space and Time:
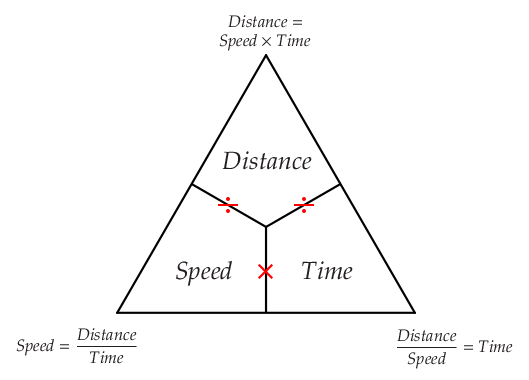
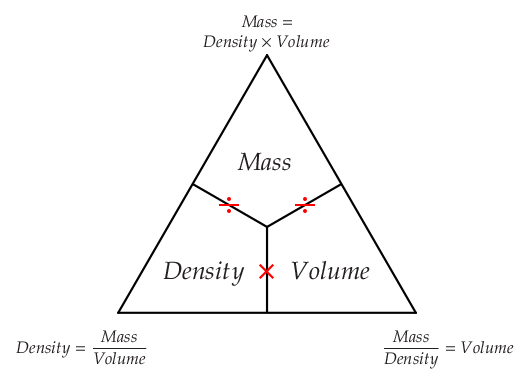
...and for those related to density:
"Mass" is an amount of matter and "volume" is an amount of Space. "Density" is usually defined as the amount of mass within a given volume.
While these relationships can be useful in some situations, they can also be extremely misleading if one is not careful. We will share a few things that we think are helpful to keep in mind:
1. Notice that "The Ohm's Law Triangle" refers only to Magnetism (
i and
E) and says nothing about Dielectricity (
I and
e).
Even when expanded into the larger "Ohm's Law Wheel", many electrical phenomena are completely absent. In general, there seems to be a gap in electrical education when it comes to the understanding of Dielectricity (or what is more commonly referred to as the "Electric Field", not to be confused with the "Electromagnetic Field"). This is compounded by the fact that some treat the science of "Electrostatics" as a historical oddity with little practical value.
2. Traditional physics focuses a lot on Space and Forward Time, whereas the concepts of Counterspace and Reverse Time might seem almost non-existent. However, "relatively unknown" does not necessarily mean "useless".
For example, Counterspace is related to the branch of mathematics known as "Projective Geometry". It is useful for describing electrical phenomena as they appear within Nature. A few researchers who have explored this type of math are George Adams, Olive Whicher, Lawrence Edwards, and Nick Thomas. They have given a solid basis to the study of what Rudolf Steiner calls the "Etheric Formative Forces". Some have approached it in an intuitive, qualitative, and psychological way too (e.g.: Guenther Wachsmuth, Ernst Lehrs, et al.).
The term "Ether" is often synonymous with what we have been referring to here as "Aether". One can find a lot of work related to this subject, but it is sometimes disregarded by being labelled as "dated", "fringe", or disrespectfully, as "woo-woo". Not all of it may be of equal use in engineering, but one's patience and kindness are needed. Truth can appear anywhere and at anytime. It cannot be emphasized enough that, while humanity has definitely gained plenty of useful knowledge in the development of science, certain understandings have also become lost. And the only way to retrieve them is to be willing to carefully review what we may think we already know.
If we trace out
the history of the Aether concept, we can see why many physicists chose to discard it despite its importance within the development of electrical technology. However, what is essentially the same concept often goes by different names (e.g.: "vacuum", "spacetime", etc.), and has a tendency to be approached mathematically instead of experimentally (i.e.: "theoretical physics").
3. Analogies can help make something more clear by giving a picture to aid in visualization, or by connecting reasoning to something familiar. Yet, at the same time, they can hide important information when taken a little too literally.
For example, "Electron Theory" is partially founded upon the analogy that can be made between "The Ohm's Law Triangle" and "The Density Triangle" given above. Physicists adopted these methods because they once measured the intensity of electrical effects by how strongly they pushed upon scales, as
if electricity was a substance that could be weighed [*see "electromechanical" meters like the "
Ampere Balance"].
How can something affect matter without itself being "material"? Electricity, more than any other Natural phenomenon that humans have learned to work with, embodies a sense of the mysterious. It can gently pass like a ghost through solid objects or utterly obliterate them in a violent explosion.
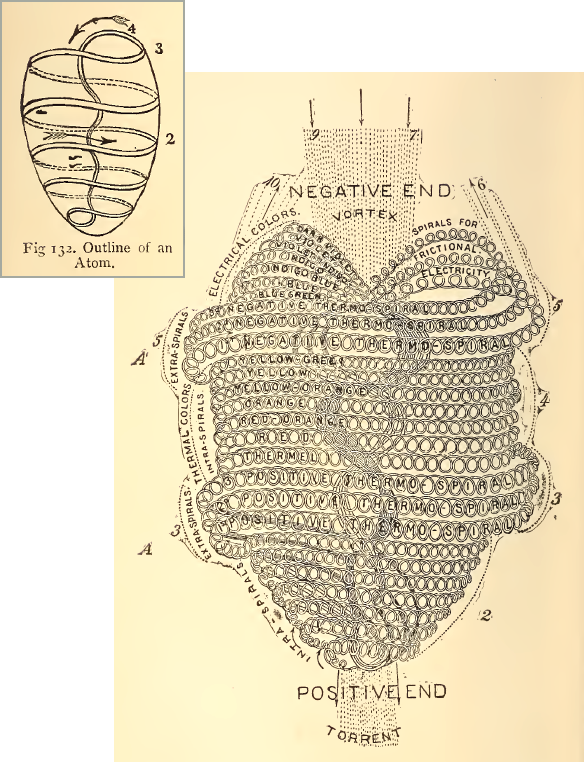
Early electrical scientists, such as Lord Kelvin, described atoms as akin to "vortices" of Aether. J.J. Thompson, and several others, developed models of "vortex atoms" throughout this period of history (around the late 1800's). And many other less well-known researchers, like
Carl Frederick Krafft, continued to develop the idea of atoms being vortices of Aether long after that time.
Diagrams from pgs. 97 and 102 of the book The Principles of Light and Color by Edwin Babbitt (circa 1896)
Up unto this day, there are several different models of the atom used interchangably within chemistry to describe various phenomena (e.g.: "electron orbitals" are used for describing the geometry of how atoms bond together and "electron shells" are used for describing the properties of different materials, such as whether it would make a good "conductor" or "insulator").
Generally, there seems to be a lot of confusion as to the "electronic structure" of the atom, and by extension, the role that various "sub-atomic particles" play within it. Just as there are many different models of atom, there are many different models for "sub-atomic particles". These are not "new" concepts either.
For example, in 1915, the chemist/physicist Alfred Parson developed
a model of the "electron" that treated it as a bundle of "electrical fibers" in a ring shape. Notice how different this is from the J.J. Thomson idea of an "electron" that we mentioned earlier (i.e.: the end of a Dielectric tube of force).
Similar to the image of the vortex atom depicted above, we might think of it as a braiding together of tubes of force. It is like an "electric field" folded in on itself, instead of appearing around or within an electrical device.
This makes clear some of the more idiosyncratic ideas about "electrons" that are found within the context of modern "quantum physics". We will quote
an interesting interview with the electronics inventor Carver Mead as another example:
So early on you knew that electrons were real.
The electrons were real, the voltages were real, the phase of the sine-wave was real, the current was real. These were real things. They were just as real as the water going down through the pipes. You listen to the technology, and you know that these things are totally real, and totally intuitive.
But they're also waves, right? Then what are they waving in?
It's interesting, isn't it? That has hung people up ever since the time of Clerk Maxwell, and it's the missing piece of intuition that we need to develop in young people. The electron isn't the disturbance of something else. It is its own thing. The electron is the thing that's wiggling, and the wave is the electron. It is its own medium. You don't need something for it to be in, because if you did it would be buffeted about and all messed up. So the only pure way to have a wave is for it to be its own medium. The electron isn't something that has a fixed physical shape. Waves propagate outwards, and they can be large or small. That's what waves do.
So how big is an electron?
It expands to fit the container it's in. That may be a positive charge that's attracting it--a hydrogen atom--or the walls of a conductor. A piece of wire is a container for electrons. They simply fill out the piece of wire. That's what all waves do. If you try to gather them into a smaller space, the energy level goes up. That's what these Copenhagen guys call the Heisenberg uncertainty principle. But there's nothing uncertain about it. It's just a property of waves. Confine them, and you have more wavelengths in a given space, and that means a higher frequency and higher energy. But a quantum wave also tends to go to the state of lowest energy, so it will expand as long as you let it. You can make an electron that's ten feet across, there's no problem with that. It's its own medium, right? And it gets to be less and less dense as you let it expand. People regularly do experiments with neutrons that are a foot across.
A ten-foot electron! Amazing.
It could be a mile. The electrons in my superconducting magnet are that long.
It is okay if this quote is not entirely clear. We just want to highlight the fact that the ideas of "electrons" that have been developed for use within chemistry and electronics are different from the ideas used by those who developed the foundations of electrical engineering. And further, because of those changes, layers of complexities have accumlated upon the situation that can make it hard to understand and duplicate some of that work.